Question Number 57348 by rajesh4661kumar@gamil.com last updated on 03/Apr/19

Commented by rajesh4661kumar@gamil.com last updated on 03/Apr/19

$${bunch}\:{of}\:{thanks} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19

$${most}\:{welcome}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19
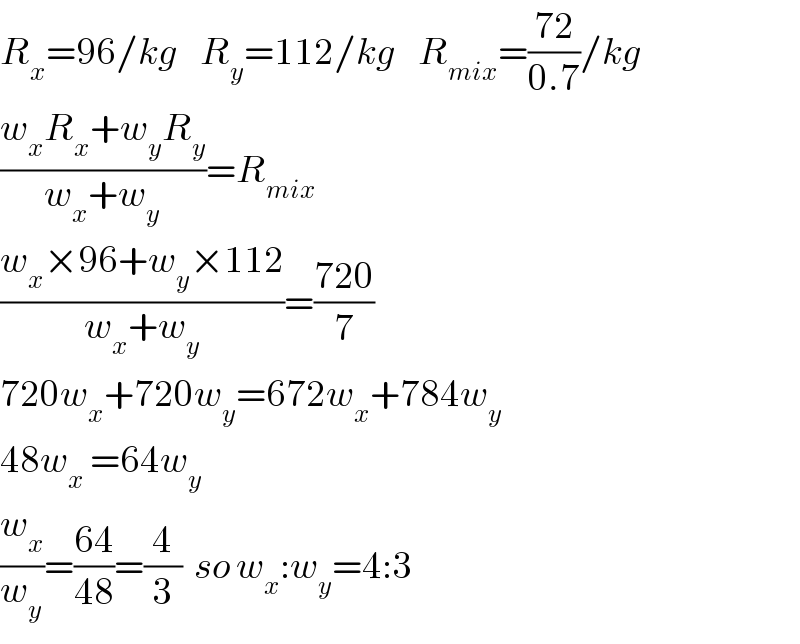
$${R}_{{x}} =\mathrm{96}/{kg}\:\:\:\:{R}_{{y}} =\mathrm{112}/{kg}\:\:\:\:{R}_{{mix}} =\frac{\mathrm{72}}{\mathrm{0}.\mathrm{7}}/{kg} \\ $$$$\frac{{w}_{{x}} {R}_{{x}} +{w}_{{y}} {R}_{{y}} }{{w}_{{x}} +{w}_{{y}} }={R}_{{mix}} \\ $$$$\frac{{w}_{{x}} ×\mathrm{96}+{w}_{{y}} ×\mathrm{112}}{{w}_{{x}} +{w}_{{y}} }=\frac{\mathrm{720}}{\mathrm{7}} \\ $$$$\mathrm{720}{w}_{{x}} +\mathrm{720}{w}_{{y}} =\mathrm{672}{w}_{{x}} +\mathrm{784}{w}_{{y}} \\ $$$$\mathrm{48}{w}_{{x}} \:=\mathrm{64}{w}_{{y}} \\ $$$$\frac{{w}_{{x}} }{{w}_{{y}} }=\frac{\mathrm{64}}{\mathrm{48}}=\frac{\mathrm{4}}{\mathrm{3}}\:\:{so}\:{w}_{{x}} :{w}_{{y}} =\mathrm{4}:\mathrm{3} \\ $$
