Menu Close

Question-57383

Tinku Tara 0 Comments
Pin




Question Number 57383 by Tinkutara last updated on 03/Apr/19
Commented by Tinkutara last updated on 03/Apr/19
B part
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19
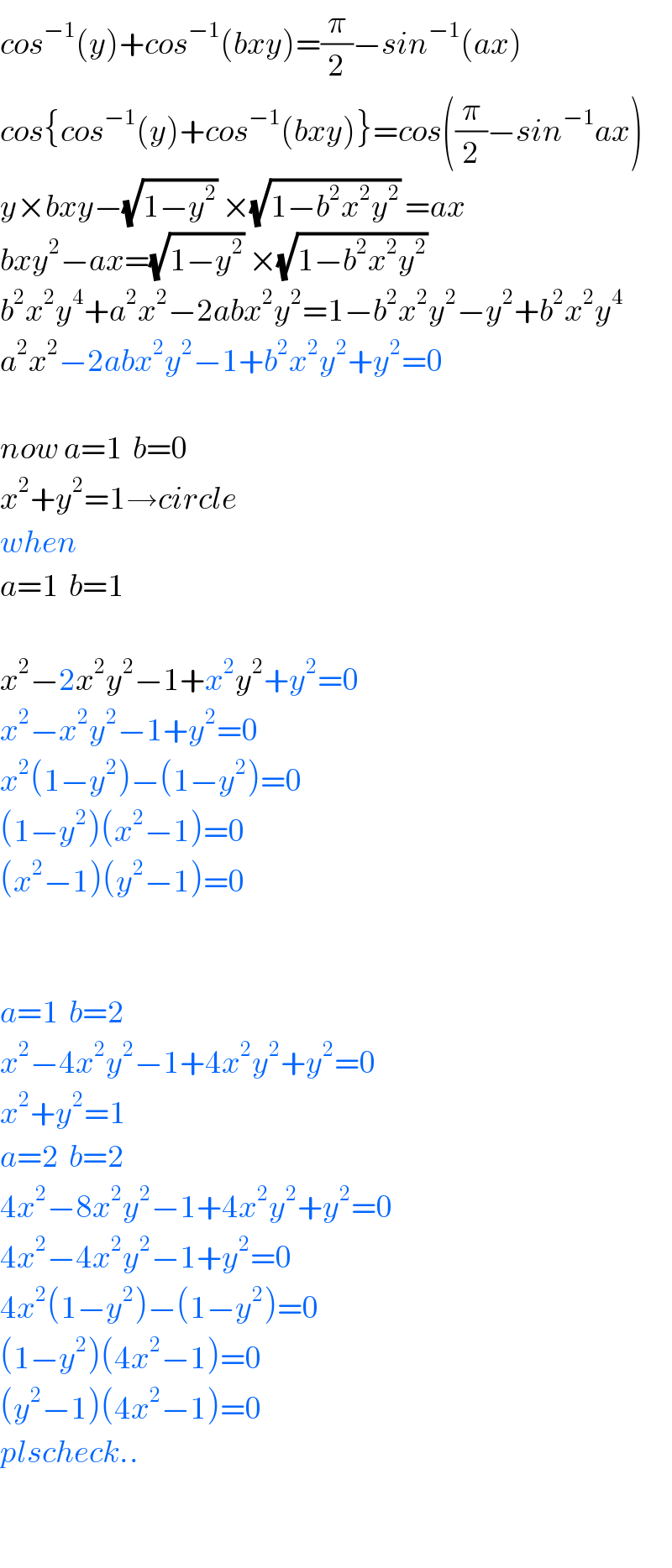
cos^(−1) (y)+cos^(−1) (bxy)=(π/2)−sin^(−1) (ax) cos{cos^(−1) (y)+cos^(−1) (bxy)}=cos((π/2)−sin^(−1) ax) y×bxy−(√(1−y^2 )) ×(√(1−b^2 x^2 y^2 )) =ax bxy^2 −ax=(√(1−y^2 )) ×(√(1−b^2 x^2 y^2 )) b^2 x^2 y^4 +a^2 x^2 −2abx^2 y^2 =1−b^2 x^2 y^2 −y^2 +b^2 x^2 y^4 a^2 x^2 −2abx^2 y^2 −1+b^2 x^2 y^2 +y^2 =0 now a=1 b=0 x^2 +y^2 =1→circle when a=1 b=1 x^2 −2x^2 y^2 −1+x^2 y^2 +y^2 =0 x^2 −x^2 y^2 −1+y^2 =0 x^2 (1−y^2 )−(1−y^2 )=0 (1−y^2 )(x^2 −1)=0 (x^2 −1)(y^2 −1)=0 a=1 b=2 x^2 −4x^2 y^2 −1+4x^2 y^2 +y^2 =0 x^2 +y^2 =1 a=2 b=2 4x^2 −8x^2 y^2 −1+4x^2 y^2 +y^2 =0 4x^2 −4x^2 y^2 −1+y^2 =0 4x^2 (1−y^2 )−(1−y^2 )=0 (1−y^2 )(4x^2 −1)=0 (y^2 −1)(4x^2 −1)=0 plscheck..
$${cos}^{−\mathrm{1}} \left({y}\right)+{cos}^{−\mathrm{1}} \left({bxy}\right)=\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left({ax}\right) \\ $$$${cos}\left\{{cos}^{−\mathrm{1}} \left({y}\right)+{cos}^{−\mathrm{1}} \left({bxy}\right)\right\}={cos}\left(\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} {ax}\right) \\ $$$${y}×{bxy}−\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:×\sqrt{\mathrm{1}−{b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{2}} }\:={ax} \\ $$$${bxy}^{\mathrm{2}} −{ax}=\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:×\sqrt{\mathrm{1}−{b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{2}} }\: \\ $$$${b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{4}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{abx}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{1}−{b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{2}} −{y}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{4}} \\ $$$${a}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{abx}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${now}\:{a}=\mathrm{1}\:\:{b}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\rightarrow{circle} \\ $$$${when} \\ $$$${a}=\mathrm{1}\:\:{b}=\mathrm{1} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)−\left(\mathrm{1}−{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$${a}=\mathrm{1}\:\:{b}=\mathrm{2} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${a}=\mathrm{2}\:\:{b}=\mathrm{2} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)−\left(\mathrm{1}−{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({y}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${plscheck}.. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 03/Apr/19
What is wrong in my method for B part?
Commented by Tinkutara last updated on 03/Apr/19
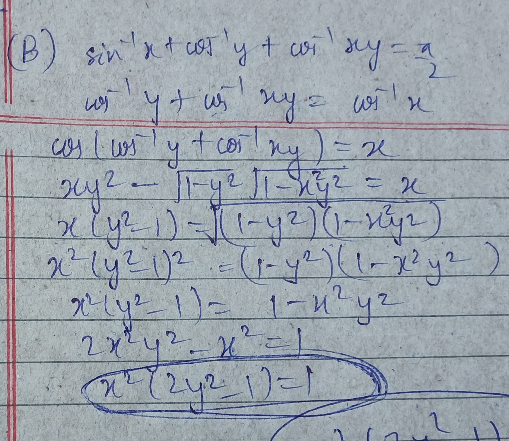
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19
x^2 (y^2 −1)^2 =(1−y^2 )(1−x^2 y^2 ) x^2 (1−y^2 )^2 =(1−y^2 )(1−x^2 y^2 ) x^2 (1−y^2 )^2 −(1−y^2 )(1−x^2 y^2 )=0 (1−y^2 )(x^2 −x^2 y^2 −1+x^2 y^2 )=0 (1−y^2 )(x^2 −1)=0 (x^2 −1)(y^2 −1)=0 now your steps x(y^2 −1)=(√((1−y^2 )(1−x^2 y^2 ))) x^2 (y^2 −1)^2 =(1−y^2 )(1−x^2 y^2 ) nxt step should be★★ but you cancelled (y^2 −1) from both side x^2 (1−y^2 )^2 −(1−y^2 )(1−x^2 y^2 )=0 since (a−b)^2 =(b−a)^2 (1−y^2 )(x^2 −x^2 y^2 −1+x^2 y^2 )=0 (1−y^2 )(x^2 −1)=0 (y^2 −1)(x^2 −1)=0
$${x}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${now}\:{your}\:{steps} \\ $$$${x}\left({y}^{\mathrm{2}} −\mathrm{1}\right)=\sqrt{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)}\: \\ $$$${x}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right) \\ $$$$\boldsymbol{{nxt}}\:\boldsymbol{{step}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\bigstar\bigstar\:\boldsymbol{{but}}\:\boldsymbol{{you}}\:\boldsymbol{{cancelled}}\:\left(\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{1}\right)\:\boldsymbol{{from}}\:\boldsymbol{{both}}\:\boldsymbol{{side}} \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} \right)\left(\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\boldsymbol{{since}}\:\left(\boldsymbol{{a}}−\boldsymbol{{b}}\right)^{\mathrm{2}} =\left(\boldsymbol{{b}}−\boldsymbol{{a}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} \right)\left(\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} −\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} \right)\left(\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{1}\right)\left(\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$
Commented by Tinkutara last updated on 03/Apr/19
Thank you so much Sir! I was confused with it for long!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *