Question Number 57385 by Tinkutara last updated on 03/Apr/19
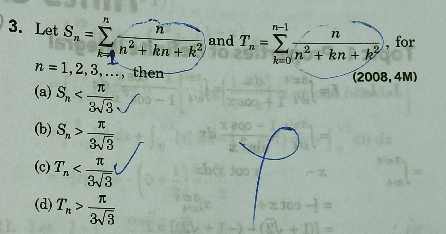
Commented by Tinkutara last updated on 03/Apr/19
How to prove d?
Answered by einsteindrmaths@hotmail.fr last updated on 03/Apr/19
![S_n <Σ_0 ^∞ (n/(n^2 +kn+k^2 ))=lim_(n→∞) Σ_0 ^n (n/(n^2 +kn+k^2 ))=lim_(n→∞) (1/n)Σ_0 ^n (1/(1+(k/n)+((k/n))^2 )) =∫_0 ^1 (1/(1+x+x^2 ))=∫_0 ^1 (1/((x+(1/2))^2 +(3/4)))=(2/( (√3)))tan^(−1) [(2/( (√3)))+(2/(2(√3)))]−(2/( (√3)))tan^(−1) [(2/(2(√3)))]<(2/( (√3)))tan^(−1) ((√(3)))](https://www.tinkutara.com/question/Q57391.png)
$${S}_{{n}} <\underset{\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}}{{n}^{\mathrm{2}} +{kn}+{k}^{\mathrm{2}} }={lim}_{{n}\rightarrow\infty} \:\underset{\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}}{{n}^{\mathrm{2}} +{kn}+{k}^{\mathrm{2}} }={lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\underset{\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}}\right]−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}}\right]<\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\sqrt{\left.\mathrm{3}\right)}\right. \\ $$
Commented by Tinkutara last updated on 03/Apr/19
Sir please prove d option, I already got a
