Question Number 57494 by bshahid010@gmail.com last updated on 05/Apr/19

Commented by MJS last updated on 06/Apr/19
![11^(cos x −sin x) =11^((√2)cos (x+(π/4))) 11^(sin x −cos x) =11^(−(√2)cos (x+(π/4))) (√2)(cos x +sin x)=2sin (x+(π/4)) the range of the 1^(st) and 2^(nd) is [11^(−(√2)) ; 11^(√2) ] ≈ ≈[.033670; 29.700] the range of the sum of these is [2; 11^(−(√2)) +11^(√2) ]≈ ≈[2; 29.733] the range of the 3^(rd) is [−2; 2] ⇒ no other solutions are possible](https://www.tinkutara.com/question/Q57504.png)
$$\mathrm{11}^{\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}} =\mathrm{11}^{\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\mathrm{11}^{\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}} =\mathrm{11}^{−\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\sqrt{\mathrm{2}}\left(\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}\right)=\mathrm{2sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{and}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{is}\:\left[\mathrm{11}^{−\sqrt{\mathrm{2}}} ;\:\mathrm{11}^{\sqrt{\mathrm{2}}} \right]\:\approx \\ $$$$\approx\left[.\mathrm{033670};\:\mathrm{29}.\mathrm{700}\right] \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{these}\:\mathrm{is}\:\left[\mathrm{2};\:\mathrm{11}^{−\sqrt{\mathrm{2}}} +\mathrm{11}^{\sqrt{\mathrm{2}}} \right]\approx \\ $$$$\approx\left[\mathrm{2};\:\mathrm{29}.\mathrm{733}\right] \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{is}\:\left[−\mathrm{2};\:\mathrm{2}\right] \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{possible} \\ $$
Answered by MJS last updated on 05/Apr/19
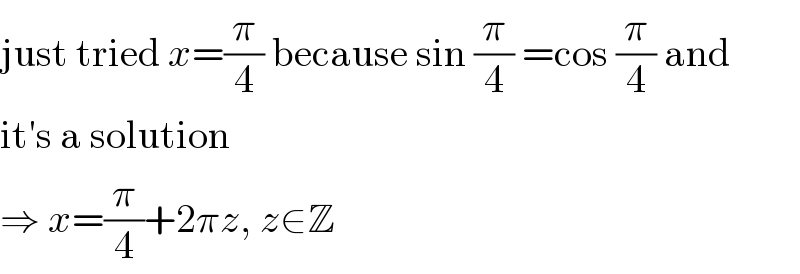
$$\mathrm{just}\:\mathrm{tried}\:{x}=\frac{\pi}{\mathrm{4}}\:\mathrm{because}\:\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\:=\mathrm{cos}\:\frac{\pi}{\mathrm{4}}\:\mathrm{and} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\Rightarrow\:{x}=\frac{\pi}{\mathrm{4}}+\mathrm{2}\pi{z},\:{z}\in\mathbb{Z} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Apr/19

$${excellent}…{sir} \\ $$
