Question Number 57521 by rahul 19 last updated on 06/Apr/19

Commented by rahul 19 last updated on 06/Apr/19

$${Ans}−\left({a}\right)\mathrm{11}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Apr/19
![T_n =x^2 +nx+(n−1)x+(n^2 −n) T_n =x^2 +(2n−1)x+(n^2 −n) T_1 =x^2 +(2.1−1)x+(1^2 −1) T_2 =x^2 +(2.2−1)x+(2^2 −2) T_3 =x^2 +(2.3−1)x+(3^2 −3) ... ... on addition ΣT_n =nx^2 +[2.(n/2){2.1+(n−1)1}−n]x+((n(n+1)(2n+1))/6)−((n(n+1))/2) =nx^2 +[n(n+1)−n]x+((n(n+1))/2)(((2n+1)/3)−1) =nx^2 +(n^2 x)+((n(n+1))/2)(((2n−2)/3)) =nx^2 +n^2 x+(n/3)(n^2 −1) so the eqn is nx^2 +n^2 x+(n/3)(n^2 −1)=10n x^2 +nx+((n^2 −1)/3)−10=0 given β=α+1 (α−β)^2 =(α+β)^2 −4αβ 1=(−n)^2 −4[((n^2 −1)/3)−10] 1=n^2 −4(((n^2 −1−30)/3)) 3=3n^2 −4n^2 +124 n^2 =121 n=11](https://www.tinkutara.com/question/Q57533.png)
$${T}_{{n}} ={x}^{\mathrm{2}} +{nx}+\left({n}−\mathrm{1}\right){x}+\left({n}^{\mathrm{2}} −{n}\right) \\ $$$${T}_{{n}} ={x}^{\mathrm{2}} +\left(\mathrm{2}{n}−\mathrm{1}\right){x}+\left({n}^{\mathrm{2}} −{n}\right) \\ $$$${T}_{\mathrm{1}} ={x}^{\mathrm{2}} +\left(\mathrm{2}.\mathrm{1}−\mathrm{1}\right){x}+\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${T}_{\mathrm{2}} ={x}^{\mathrm{2}} +\left(\mathrm{2}.\mathrm{2}−\mathrm{1}\right){x}+\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$${T}_{\mathrm{3}} ={x}^{\mathrm{2}} +\left(\mathrm{2}.\mathrm{3}−\mathrm{1}\right){x}+\left(\mathrm{3}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$… \\ $$$$… \\ $$$${on}\:{addition} \\ $$$$\Sigma{T}_{{n}} ={nx}^{\mathrm{2}} +\left[\mathrm{2}.\frac{{n}}{\mathrm{2}}\left\{\mathrm{2}.\mathrm{1}+\left({n}−\mathrm{1}\right)\mathrm{1}\right\}−{n}\right]{x}+\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$={nx}^{\mathrm{2}} +\left[{n}\left({n}+\mathrm{1}\right)−{n}\right]{x}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right) \\ $$$$={nx}^{\mathrm{2}} +\left({n}^{\mathrm{2}} {x}\right)+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}−\mathrm{2}}{\mathrm{3}}\right) \\ $$$$={nx}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}+\frac{{n}}{\mathrm{3}}\left({n}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${so}\:{the}\:{eqn}\:{is} \\ $$$${nx}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}+\frac{{n}}{\mathrm{3}}\left({n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{10}{n} \\ $$$${x}^{\mathrm{2}} +{nx}+\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}−\mathrm{10}=\mathrm{0} \\ $$$${given}\:\beta=\alpha+\mathrm{1} \\ $$$$\left(\alpha−\beta\right)^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta \\ $$$$\mathrm{1}=\left(−{n}\right)^{\mathrm{2}} −\mathrm{4}\left[\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}−\mathrm{10}\right] \\ $$$$\mathrm{1}={n}^{\mathrm{2}} −\mathrm{4}\left(\frac{{n}^{\mathrm{2}} −\mathrm{1}−\mathrm{30}}{\mathrm{3}}\right) \\ $$$$\mathrm{3}=\mathrm{3}{n}^{\mathrm{2}} −\mathrm{4}{n}^{\mathrm{2}} +\mathrm{124} \\ $$$${n}^{\mathrm{2}} =\mathrm{121} \\ $$$${n}=\mathrm{11} \\ $$$$ \\ $$$$ \\ $$
Commented by rahul 19 last updated on 07/Apr/19

$${thanks}\:{sir}! \\ $$
Commented by peter frank last updated on 07/Apr/19

$${thank}\:{you} \\ $$
Answered by Rasheed.Sindhi last updated on 07/Apr/19
![x(x+1)+(x+1)(x+2)+...(x+n−1^(−) )(x+n)=10n nx^2 +n^2 x+(n/3)(n^2 −1)=10n [ From tanmay sir] Let α & (α+1) are solutions: α(α+1)+(α+1)(α+2)+...(α+n−1^(−) )(α+n)=10n...(I) (α+1)(α+2)+(α+2)(α+3)...(α+n)(α+n+1^(−) )=10n...(II) (I)−(II): α(α+1)−(α+n)(α+n+1)=0 α^2 +α−[α^2 +(2n+1)α+n(n+1)]=0 −2nα−n^2 −n=0 n^2 +(2α+1)n=0 n(n+2α+1)=0 As n>0 ⇒n+2α+1=0 n=−2α−1 According the guidance of sir mr W: α=−((n+1)/2) Putting in (I) (-((n+1)/2))(-((n+1)/2)+1)+(-((n+1)/2)+1)(-((n+1)/2)+2)+...(-((n+1)/2)+n−1^(−) )(-((n+1)/2)+n)=10n...(I) Or equivalently according to sir tanmay n(-((n+1)/2))^2 +n^2 (-((n+1)/2))+(n/3)(n^2 −1)=10n ((n(n+1)^2 )/4)−((n^2 (n+1))/2)+((n(n^2 −1))/3)=10n 3n(n+1)^2 −6n^2 (n+1)+4n(n^2 −1)=120n 3n^3 +6n^2 +3n−6n^3 −6n^2 +4n^3 −4n−120n=0 n^3 −121n=0 n(n^2 −121)=0 ∵ n>0⇒n^2 =121⇒n=11](https://www.tinkutara.com/question/Q57540.png)
$${x}\left({x}+\mathrm{1}\right)+\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)+…\left({x}+\overline {{n}−\mathrm{1}}\right)\left({x}+{n}\right)=\mathrm{10}{n} \\ $$$${nx}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}+\frac{{n}}{\mathrm{3}}\left({n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{10}{n} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\:{From}\:{tanmay}\:{sir}\right] \\ $$$${Let}\:\alpha\:\&\:\left(\alpha+\mathrm{1}\right)\:{are}\:{solutions}: \\ $$$$\alpha\left(\alpha+\mathrm{1}\right)+\left(\alpha+\mathrm{1}\right)\left(\alpha+\mathrm{2}\right)+…\left(\alpha+\overline {{n}−\mathrm{1}}\right)\left(\alpha+{n}\right)=\mathrm{10}{n}…\left({I}\right) \\ $$$$\left(\alpha+\mathrm{1}\right)\left(\alpha+\mathrm{2}\right)+\left(\alpha+\mathrm{2}\right)\left(\alpha+\mathrm{3}\right)…\left(\alpha+{n}\right)\left(\alpha+\overline {{n}+\mathrm{1}}\right)=\mathrm{10}{n}…\left({II}\right) \\ $$$$\left({I}\right)−\left({II}\right): \\ $$$$\alpha\left(\alpha+\mathrm{1}\right)−\left(\alpha+{n}\right)\left(\alpha+{n}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\alpha−\left[\alpha^{\mathrm{2}} +\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha+{n}\left({n}+\mathrm{1}\right)\right]=\mathrm{0} \\ $$$$−\mathrm{2}{n}\alpha−{n}^{\mathrm{2}} −{n}=\mathrm{0} \\ $$$${n}^{\mathrm{2}} +\left(\mathrm{2}\alpha+\mathrm{1}\right){n}=\mathrm{0} \\ $$$${n}\left({n}+\mathrm{2}\alpha+\mathrm{1}\right)=\mathrm{0} \\ $$$${As}\:\:{n}>\mathrm{0}\:\Rightarrow{n}+\mathrm{2}\alpha+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:{n}=−\mathrm{2}\alpha−\mathrm{1} \\ $$$${According}\:{the}\:{guidance}\:{of}\:{sir}\:{mr}\:{W}: \\ $$$$\alpha=−\frac{{n}+\mathrm{1}}{\mathrm{2}} \\ $$$${Putting}\:{in}\:\left({I}\right) \\ $$$$\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)+\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right)+…\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}+\overline {{n}−\mathrm{1}}\right)\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}+{n}\right)=\mathrm{10}{n}…\left({I}\right) \\ $$$${Or}\:{equivalently}\:{according}\:{to}\:{sir}\:{tanmay}\: \\ $$$$\:{n}\left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} \left(-\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)+\frac{{n}}{\mathrm{3}}\left({n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{10}{n} \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}{\mathrm{2}}+\frac{{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{3}}=\mathrm{10}{n} \\ $$$$\mathrm{3}{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)+\mathrm{4}{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{120}{n} \\ $$$$\mathrm{3}{n}^{\mathrm{3}} +\mathrm{6}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{6}{n}^{\mathrm{3}} −\mathrm{6}{n}^{\mathrm{2}} +\mathrm{4}{n}^{\mathrm{3}} −\mathrm{4}{n}−\mathrm{120}{n}=\mathrm{0} \\ $$$${n}^{\mathrm{3}} −\mathrm{121}{n}=\mathrm{0} \\ $$$${n}\left({n}^{\mathrm{2}} −\mathrm{121}\right)=\mathrm{0} \\ $$$$\because\:{n}>\mathrm{0}\Rightarrow{n}^{\mathrm{2}} =\mathrm{121}\Rightarrow{n}=\mathrm{11} \\ $$
Commented by mr W last updated on 07/Apr/19
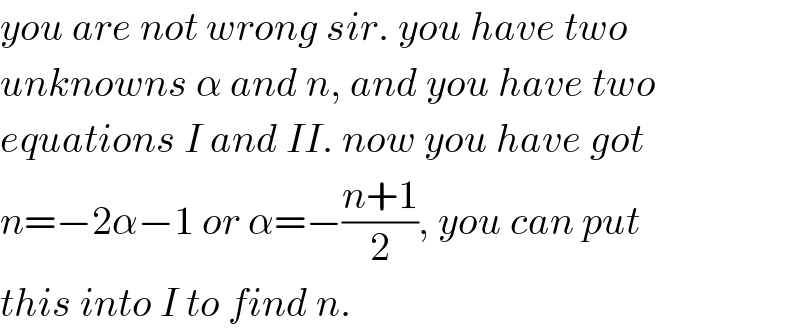
$${you}\:{are}\:{not}\:{wrong}\:{sir}.\:{you}\:{have}\:{two} \\ $$$${unknowns}\:\alpha\:{and}\:{n},\:{and}\:{you}\:{have}\:{two} \\ $$$${equations}\:{I}\:{and}\:{II}.\:{now}\:{you}\:{have}\:{got} \\ $$$${n}=−\mathrm{2}\alpha−\mathrm{1}\:{or}\:\alpha=−\frac{{n}+\mathrm{1}}{\mathrm{2}},\:{you}\:{can}\:{put} \\ $$$${this}\:{into}\:{I}\:{to}\:{find}\:{n}. \\ $$
Commented by Rasheed.Sindhi last updated on 07/Apr/19
$$\theta{NX}\:\:\:{S}\:{i}\mathcal{R}\:{mr}\:{W}! \\ $$
