Question Number 57602 by MJS last updated on 08/Apr/19
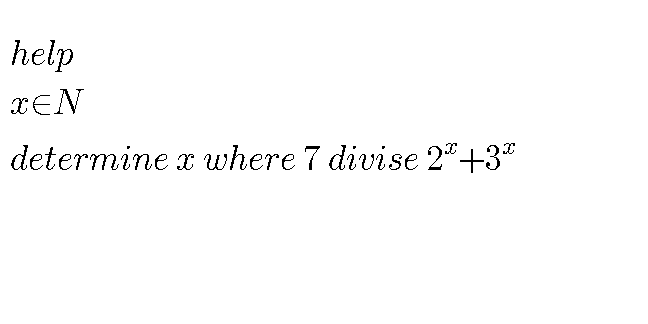
Commented by MJS last updated on 08/Apr/19

$$\mathrm{reposted}\:\mathrm{qu}.\:\mathrm{21795} \\ $$
Answered by MJS last updated on 08/Apr/19

$$\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$$$\mathrm{the}\:\mathrm{remainders}\:\mathrm{of}\:\frac{\mathrm{2}^{{x}} }{\mathrm{7}}\:\mathrm{with}\:{x}\in\mathbb{N}: \\ $$$$\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:…\right\} \\ $$$$\mathrm{the}\:\mathrm{remainders}\:\mathrm{of}\:\frac{\mathrm{3}^{{x}} }{\mathrm{7}}\:\mathrm{with}\:{x}\in\mathbb{N}: \\ $$$$\left\{\mathrm{1},\:\mathrm{3},\:\mathrm{2},\:\mathrm{6},\:\mathrm{4},\:\mathrm{5},\:\mathrm{1},\:\mathrm{3},\:\mathrm{2},\:\mathrm{6},\:\mathrm{4},\:\mathrm{5},\:…\right\} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{these}: \\ $$$$\left\{\mathrm{2},\:\mathrm{5},\:\mathrm{6},\:\mathrm{7},\:\mathrm{6},\:\mathrm{2},\:\mathrm{2},\:\mathrm{5},\:\mathrm{6},\:\mathrm{7},\:\mathrm{6},\:\mathrm{2},\:\:…\right\} \\ $$$$\Rightarrow\:{x}=\mathrm{3}+\mathrm{6}{n} \\ $$
Commented by mr W last updated on 08/Apr/19
$${very}\:{nice}\:{approach}\:{sir}! \\ $$
Commented by MJS last updated on 08/Apr/19

$$\mathrm{thank}\:\mathrm{you}.\:\mathrm{I}\:\mathrm{was}\:\mathrm{just}\:\mathrm{trying}… \\ $$
Commented by mr W last updated on 09/Apr/19
$${i}\:{got}\:{the}\:{same}\:{result}\:{x}=\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right),\:{but} \\ $$$${i}\:{was}\:{not}\:{sure}\:{if}\:{there}\:{are}\:{other}\:{solutions}. \\ $$
