Question Number 57669 by rahul 19 last updated on 09/Apr/19

Commented by mr W last updated on 09/Apr/19
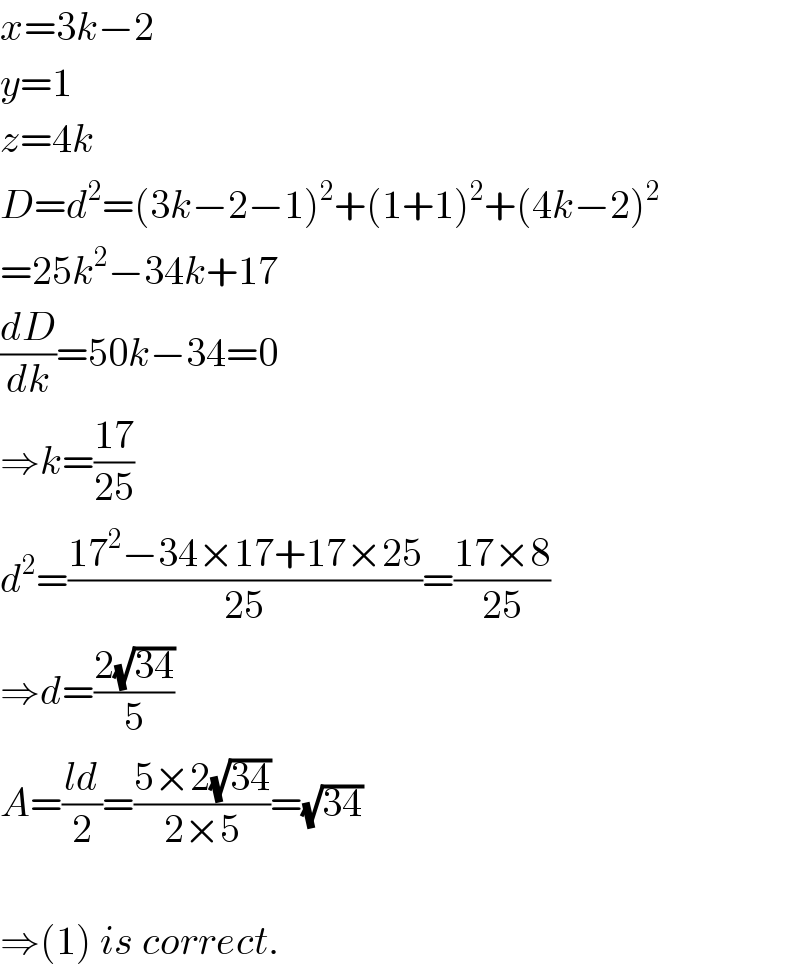
$${x}=\mathrm{3}{k}−\mathrm{2} \\ $$$${y}=\mathrm{1} \\ $$$${z}=\mathrm{4}{k} \\ $$$${D}={d}^{\mathrm{2}} =\left(\mathrm{3}{k}−\mathrm{2}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{4}{k}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$=\mathrm{25}{k}^{\mathrm{2}} −\mathrm{34}{k}+\mathrm{17} \\ $$$$\frac{{dD}}{{dk}}=\mathrm{50}{k}−\mathrm{34}=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\mathrm{17}}{\mathrm{25}} \\ $$$${d}^{\mathrm{2}} =\frac{\mathrm{17}^{\mathrm{2}} −\mathrm{34}×\mathrm{17}+\mathrm{17}×\mathrm{25}}{\mathrm{25}}=\frac{\mathrm{17}×\mathrm{8}}{\mathrm{25}} \\ $$$$\Rightarrow{d}=\frac{\mathrm{2}\sqrt{\mathrm{34}}}{\mathrm{5}} \\ $$$${A}=\frac{{ld}}{\mathrm{2}}=\frac{\mathrm{5}×\mathrm{2}\sqrt{\mathrm{34}}}{\mathrm{2}×\mathrm{5}}=\sqrt{\mathrm{34}} \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{1}\right)\:{is}\:{correct}. \\ $$
Commented by rahul 19 last updated on 09/Apr/19
thank you sir!
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Apr/19

$$\frac{{x}+\mathrm{2}}{\mathrm{3}}=\frac{{y}−\mathrm{1}}{\mathrm{0}}=\frac{{z}}{\mathrm{4}}={r} \\ $$$${pointD}\left\{\left(\mathrm{3}{r}−\mathrm{2}\right),\mathrm{1},\mathrm{4}{r}\right\}{lies}\:{on}\:{given}\:{st}\:{line} \\ $$$${direction}\:{ratio}\:{betweenA}\:\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right)\:{andD}\left\{\left(\mathrm{3}{r}−\mathrm{2}\right),\mathrm{1},\mathrm{4}{r}\right\} \\ $$$${is}\:\left\{\mathrm{3}{r}−\mathrm{3},\mathrm{2},\mathrm{4}{r}−\mathrm{2}\right\} \\ $$$${AD}\bot{given}\left[{st}\:{line}\right. \\ $$$$\left(\mathrm{3}{r}−\mathrm{3}\right)×\mathrm{3}+\mathrm{2}×\mathrm{0}+\left(\mathrm{4}{r}−\mathrm{2}\right)×\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{9}{r}−\mathrm{9}+\mathrm{16}{r}−\mathrm{8}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{17}}{\mathrm{25}} \\ $$$${point}\:{D}\left\{\mathrm{3}{r}−\mathrm{2},\mathrm{1},\mathrm{4}{r}\right\}\rightarrow\left\{\frac{\mathrm{51}}{\mathrm{25}}−\mathrm{2},\mathrm{1},\frac{\mathrm{68}}{\mathrm{25}}\right\} \\ $$$${PointD}=\left\{\frac{\mathrm{1}}{\mathrm{25}},\mathrm{1},\frac{\mathrm{68}}{\mathrm{25}}\right\} \\ $$$${distance}\:{between}\:{AD}=\sqrt{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{25}}\right)^{\mathrm{2}} +\left(−\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}−\frac{\mathrm{68}}{\mathrm{25}}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\frac{\mathrm{576}}{\mathrm{625}}+\mathrm{4}+\frac{\mathrm{324}}{\mathrm{625}}} \\ $$$$=\sqrt{\frac{\mathrm{576}+\mathrm{2500}+\mathrm{324}}{\mathrm{625}}}\: \\ $$$$=\sqrt{\frac{\mathrm{3400}}{\mathrm{625}}}\:=\sqrt{\frac{\mathrm{34}×\mathrm{4}}{\mathrm{25}}\:}\:=\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\mathrm{34}}\: \\ $$$${area}\:{of}\:{triangle}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\mathrm{34}}\:×\mathrm{5}=\sqrt{\mathrm{34}}\:{unit} \\ $$
Commented by rahul 19 last updated on 09/Apr/19
thank you sir!
