Question-57698

Question Number 57698 by rahul 19 last updated on 10/Apr/19

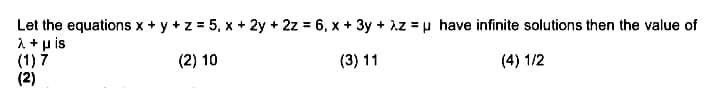
Commented by rahul 19 last updated on 10/Apr/19

3rd plane can be written as : P_1 +ΥP_2 , how to find Υ? here λ=3,μ=7 but then Υ is not unique!

$$\mathrm{3}{rd}\:{plane}\:{can}\:{be}\:{written}\:{as}\:: \\ $$$${P}_{\mathrm{1}} +\Upsilon{P}_{\mathrm{2}} \:,\:{how}\:{to}\:{find}\:\:\Upsilon? \\ $$$${here}\:\lambda=\mathrm{3},\mu=\mathrm{7}\:{but}\:{then}\:\Upsilon\:{is}\:{not}\:{unique}! \\ $$

Answered by mr W last updated on 10/Apr/19

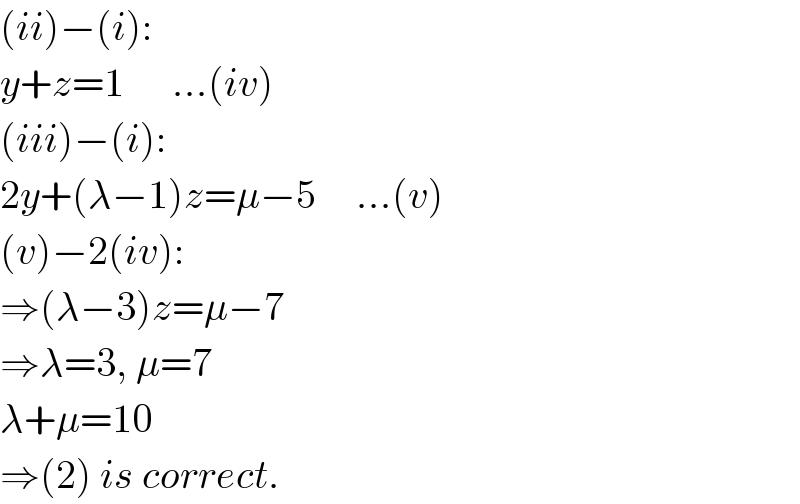
(ii)−(i): y+z=1 ...(iv) (iii)−(i): 2y+(λ−1)z=μ−5 ...(v) (v)−2(iv): ⇒(λ−3)z=μ−7 ⇒λ=3, μ=7 λ+μ=10 ⇒(2) is correct.

$$\left({ii}\right)−\left({i}\right): \\ $$$${y}+{z}=\mathrm{1}\:\:\:\:\:\:…\left({iv}\right) \\ $$$$\left({iii}\right)−\left({i}\right): \\ $$$$\mathrm{2}{y}+\left(\lambda−\mathrm{1}\right){z}=\mu−\mathrm{5}\:\:\:\:\:…\left({v}\right) \\ $$$$\left({v}\right)−\mathrm{2}\left({iv}\right): \\ $$$$\Rightarrow\left(\lambda−\mathrm{3}\right){z}=\mu−\mathrm{7} \\ $$$$\Rightarrow\lambda=\mathrm{3},\:\mu=\mathrm{7} \\ $$$$\lambda+\mu=\mathrm{10} \\ $$$$\Rightarrow\left(\mathrm{2}\right)\:{is}\:{correct}. \\ $$

Commented by rahul 19 last updated on 10/Apr/19

Sir, what's the problem in my method?

Commented by mr W last updated on 10/Apr/19

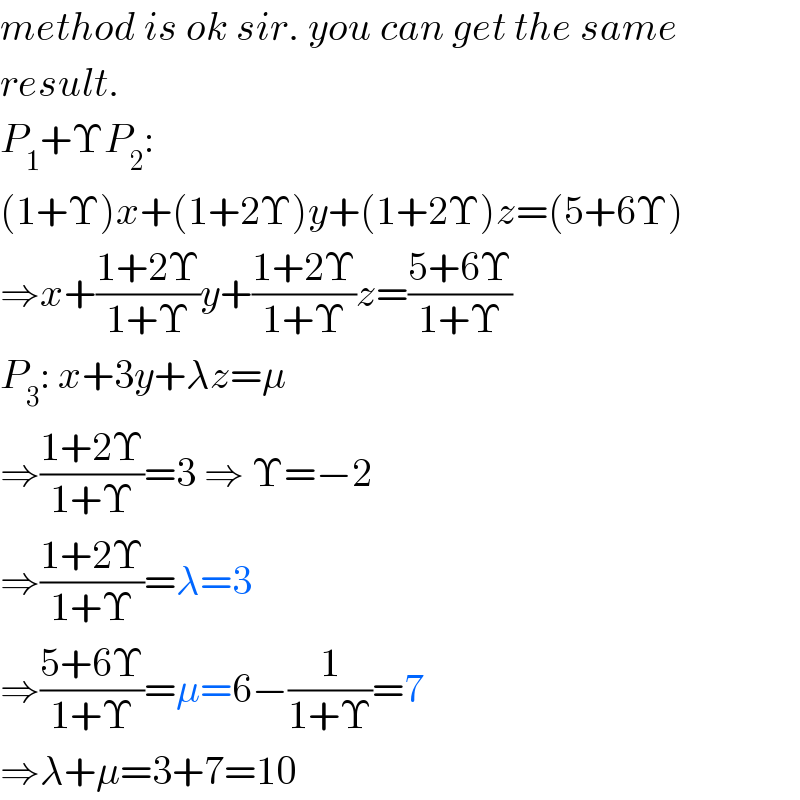
method is ok sir. you can get the same result. P_1 +ΥP_2 : (1+Υ)x+(1+2Υ)y+(1+2Υ)z=(5+6Υ) ⇒x+((1+2Υ)/(1+Υ))y+((1+2Υ)/(1+Υ))z=((5+6Υ)/(1+Υ)) P_3 : x+3y+λz=μ ⇒((1+2Υ)/(1+Υ))=3 ⇒ Υ=−2 ⇒((1+2Υ)/(1+Υ))=λ=3 ⇒((5+6Υ)/(1+Υ))=μ=6−(1/(1+Υ))=7 ⇒λ+μ=3+7=10

$${method}\:{is}\:{ok}\:{sir}.\:{you}\:{can}\:{get}\:{the}\:{same} \\ $$$${result}. \\ $$$${P}_{\mathrm{1}} +\Upsilon{P}_{\mathrm{2}} : \\ $$$$\left(\mathrm{1}+\Upsilon\right){x}+\left(\mathrm{1}+\mathrm{2}\Upsilon\right){y}+\left(\mathrm{1}+\mathrm{2}\Upsilon\right){z}=\left(\mathrm{5}+\mathrm{6}\Upsilon\right) \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}+\mathrm{2}\Upsilon}{\mathrm{1}+\Upsilon}{y}+\frac{\mathrm{1}+\mathrm{2}\Upsilon}{\mathrm{1}+\Upsilon}{z}=\frac{\mathrm{5}+\mathrm{6}\Upsilon}{\mathrm{1}+\Upsilon} \\ $$$${P}_{\mathrm{3}} :\:{x}+\mathrm{3}{y}+\lambda{z}=\mu \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{2}\Upsilon}{\mathrm{1}+\Upsilon}=\mathrm{3}\:\Rightarrow\:\Upsilon=−\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{2}\Upsilon}{\mathrm{1}+\Upsilon}=\lambda=\mathrm{3} \\ $$$$\Rightarrow\frac{\mathrm{5}+\mathrm{6}\Upsilon}{\mathrm{1}+\Upsilon}=\mu=\mathrm{6}−\frac{\mathrm{1}}{\mathrm{1}+\Upsilon}=\mathrm{7} \\ $$$$\Rightarrow\lambda+\mu=\mathrm{3}+\mathrm{7}=\mathrm{10} \\ $$

Commented by rahul 19 last updated on 11/Apr/19

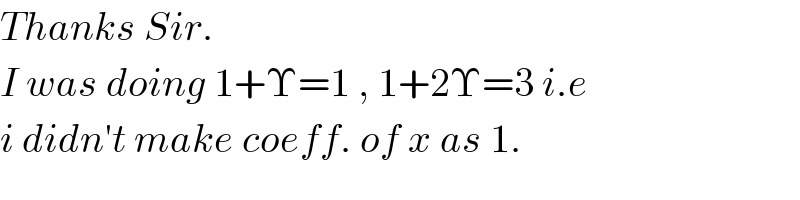
Thanks Sir. I was doing 1+Υ=1 , 1+2Υ=3 i.e i didn′t make coeff. of x as 1.

$${Thanks}\:{Sir}. \\ $$$${I}\:{was}\:{doing}\:\mathrm{1}+\Upsilon=\mathrm{1}\:,\:\mathrm{1}+\mathrm{2}\Upsilon=\mathrm{3}\:{i}.{e} \\ $$$${i}\:{didn}'{t}\:{make}\:{coeff}.\:{of}\:{x}\:{as}\:\mathrm{1}. \\ $$

Commented by mr W last updated on 11/Apr/19

$${the}\:{coefficients}\:{must}\:{not}\:{be}\:{the}\:{same}, \\ $$$${only}\:{the}\:{ratios}\:{between}\:{them}\:{must}\:{be} \\ $$$${the}\:{same}.\: \\ $$

Commented by rahul 19 last updated on 11/Apr/19

$$\left.{Ok}\:{Sir}!:\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply