Menu Close

Question-57770

Tinku Tara 0 Comments
Pin




Question Number 57770 by Tawa1 last updated on 11/Apr/19
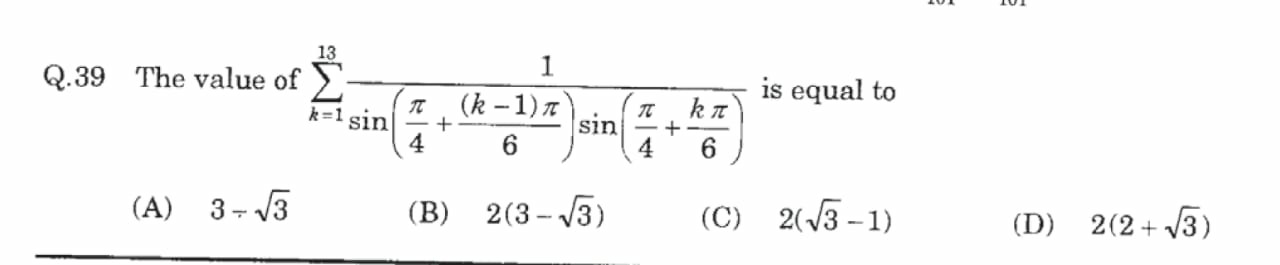
Answered by Kunal12588 last updated on 11/Apr/19
Σ_(k=1) ^(13) (1/(sin((π/4)+(((k−1)π)/6))sin((π/4)+((kπ)/6)))) sin((π/4)+(((k−1)π)/6))sin((π/4)+((kπ)/6)) =sin(((3π+2(k−1)π)/(12)))sin(((3π+2kπ)/(12))) =sin((((2k+1)π)/(12)))sin((((2k+3)π)/(12))) =(1/2){cos((((2k+3)π−(2k+1)π)/(12)))−cos((((2k+3)π+(2k+1)π)/(12)))} =(1/2){cos(((2π)/(12)))−cos(((4k+4)π)/(12))} =(1/2){cos(π/6)−cos((k+1)/3)π} =(1/2){((√3)/2)−cos((k+1)/3)π} k=1,2,3,4,5,6,7,8,9,10,11,12,13 ((k+1)/3)=(2/3),1,1(1/3),1(2/3),2,2(1/3),2(2/3),3,3(1/3),3(2/3),4,4(1/3),4(2/3) cos((k+1)/3)π=c_(120°) ,c_(180) ,c_(240) ,c_(300) ,c_(360) ,c_(60) ,c_(120) ,... =−(1/2),−1,−(1/2),(1/2),1,(1/2),−(1/2),... Σ_(k=1) ^(13) (1/(sin((π/4)+(((k−1)π)/6))sin((π/4)+((kπ)/6)))) =2((4/( (√3)+1))+(4/( (√3)+2))+(4/( (√3)+1))+(4/( (√3)−1))+(4/( (√3)−2))+(4/( (√3)−1)))+(4/( (√3)+1)) =8((((√3)−1)/2)+(((√3)−2)/(−1))+(((√3)−1)/2)+(((√3)+1)/2)+(((√3)+2)/(−1))+(((√3)+1)/2))+((4((√3)−1))/2) =4((√3)−1−2(√3)+4+(√3)−1+(√3)+1−2(√3)−4+(√3)+1)+2((√3)−1) =4(0)+2((√3)−1) =2((√3)−1) Ans: C
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{4}}+\frac{\left({k}−\mathrm{1}\right)\pi}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{6}}\right)} \\ $$$${sin}\left(\frac{\pi}{\mathrm{4}}+\frac{\left({k}−\mathrm{1}\right)\pi}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{6}}\right) \\ $$$$={sin}\left(\frac{\mathrm{3}\pi+\mathrm{2}\left({k}−\mathrm{1}\right)\pi}{\mathrm{12}}\right){sin}\left(\frac{\mathrm{3}\pi+\mathrm{2}{k}\pi}{\mathrm{12}}\right) \\ $$$$={sin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right){sin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{3}\right)\pi}{\mathrm{12}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{3}\right)\pi−\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)−{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{3}\right)\pi+\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{12}}\right)−{cos}\frac{\left(\mathrm{4}{k}+\mathrm{4}\right)\pi}{\mathrm{12}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\frac{\pi}{\mathrm{6}}−{cos}\frac{{k}+\mathrm{1}}{\mathrm{3}}\pi\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−{cos}\frac{{k}+\mathrm{1}}{\mathrm{3}}\pi\right\} \\ $$$${k}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{10},\mathrm{11},\mathrm{12},\mathrm{13} \\ $$$$\frac{{k}+\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}},\mathrm{1},\mathrm{1}\frac{\mathrm{1}}{\mathrm{3}},\mathrm{1}\frac{\mathrm{2}}{\mathrm{3}},\mathrm{2},\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}},\mathrm{2}\frac{\mathrm{2}}{\mathrm{3}},\mathrm{3},\mathrm{3}\frac{\mathrm{1}}{\mathrm{3}},\mathrm{3}\frac{\mathrm{2}}{\mathrm{3}},\mathrm{4},\mathrm{4}\frac{\mathrm{1}}{\mathrm{3}},\mathrm{4}\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${cos}\frac{{k}+\mathrm{1}}{\mathrm{3}}\pi={c}_{\mathrm{120}°} ,{c}_{\mathrm{180}} ,{c}_{\mathrm{240}} ,{c}_{\mathrm{300}} ,{c}_{\mathrm{360}} ,{c}_{\mathrm{60}} ,{c}_{\mathrm{120}} ,… \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}},−\mathrm{1},−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}},−\frac{\mathrm{1}}{\mathrm{2}},… \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{4}}+\frac{\left({k}−\mathrm{1}\right)\pi}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{6}}\right)} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{2}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}−\mathrm{2}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}\right)+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$$=\mathrm{8}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}−\mathrm{2}}{−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}+\mathrm{2}}{−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{4}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\mathrm{4}\left(\sqrt{\mathrm{3}}−\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{4}+\sqrt{\mathrm{3}}−\mathrm{1}+\sqrt{\mathrm{3}}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{4}+\sqrt{\mathrm{3}}+\mathrm{1}\right)+\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$=\mathrm{4}\left(\mathrm{0}\right)+\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$=\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$${Ans}:\:{C} \\ $$
Commented by Tawa1 last updated on 11/Apr/19
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by abbas-alsadi last updated on 12/Apr/19
$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *