Menu Close

Question-57818

Tinku Tara 0 Comments
Pin




Question Number 57818 by Tawa1 last updated on 12/Apr/19
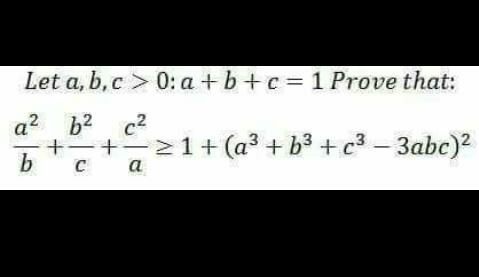
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
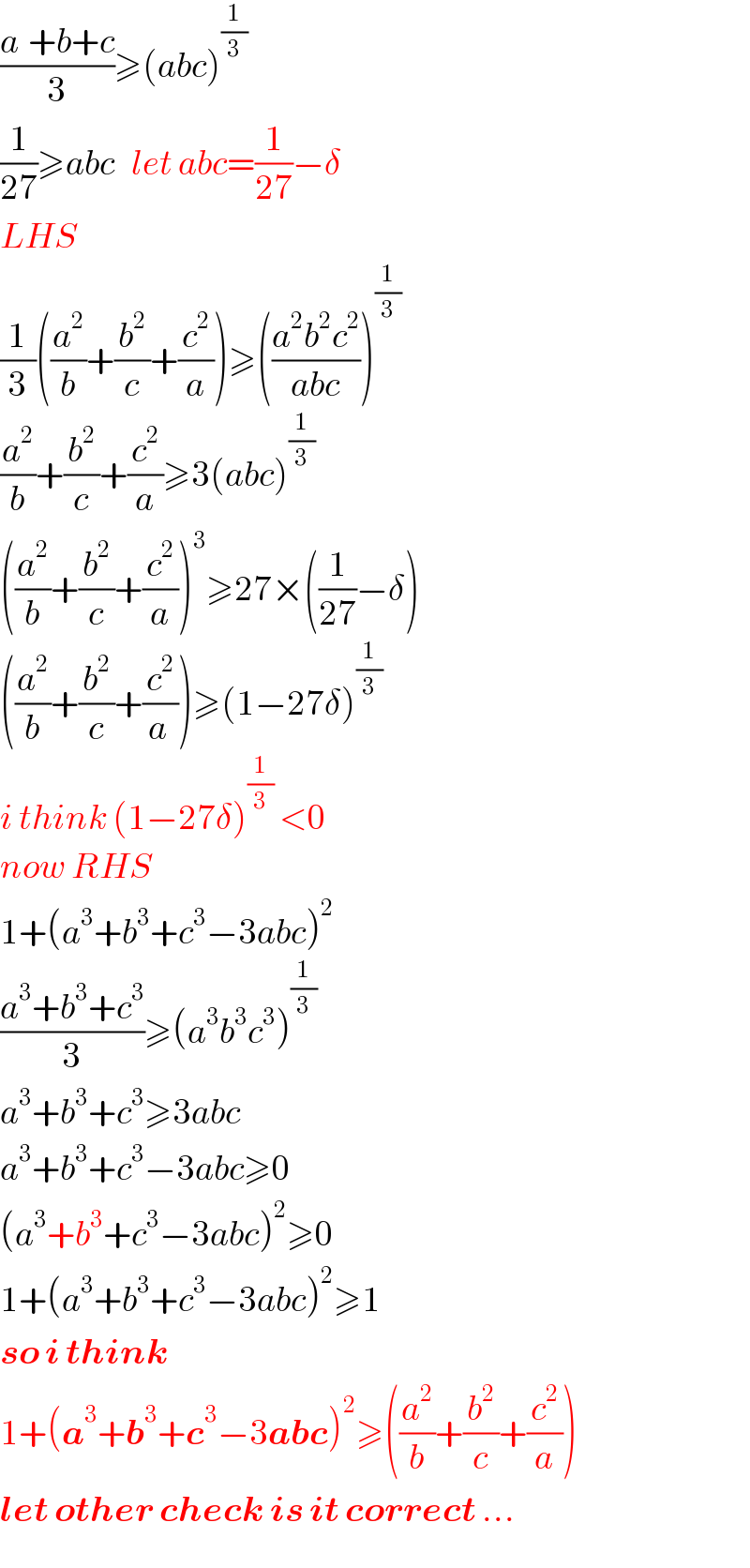
((a^ +b+c)/3)≥(abc)^(1/3) (1/(27))≥abc let abc=(1/(27))−δ LHS (1/3)((a^2 /b)+(b^2 /c)+(c^2 /a))≥(((a^2 b^2 c^2 )/(abc)))^(1/3) (a^2 /b)+(b^2 /c)+(c^2 /a)≥3(abc)^(1/3) ((a^2 /b)+(b^2 /c)+(c^2 /a))^3 ≥27×((1/(27))−δ) ((a^2 /b)+(b^2 /c)+(c^2 /(a )))≥(1−27δ)^(1/3) i think (1−27δ)^(1/3) <0 now RHS 1+(a^3 +b^3 +c^3 −3abc)^2 ((a^3 +b^3 +c^3 )/3)≥(a^3 b^3 c^3 )^(1/3) a^3 +b^3 +c^3 ≥3abc a^3 +b^3 +c^3 −3abc≥0 (a^3 +b^3 +c^3 −3abc)^2 ≥0 1+(a^3 +b^3 +c^3 −3abc)^2 ≥1 so i think 1+(a^3 +b^3 +c^3 −3abc)^2 ≥((a^2 /b)+(b^2 /c)+(c^2 /a)) let other check is it correct ...
$$\frac{{a}^{} +{b}+{c}}{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{27}}\geqslant{abc}\:\:\:{let}\:{abc}=\frac{\mathrm{1}}{\mathrm{27}}−\delta \\ $$$${LHS} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} }{{a}}\right)\geqslant\left(\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }{{abc}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} }{{a}}\geqslant\mathrm{3}\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left(\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} }{{a}}\right)^{\mathrm{3}} \geqslant\mathrm{27}×\left(\frac{\mathrm{1}}{\mathrm{27}}−\delta\right) \\ $$$$\left(\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} }{{a}\:}\right)\geqslant\left(\mathrm{1}−\mathrm{27}\delta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${i}\:{think}\:\left(\mathrm{1}−\mathrm{27}\delta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:<\mathrm{0} \\ $$$${now}\:{RHS} \\ $$$$\mathrm{1}+\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\right)^{\mathrm{2}} \\ $$$$\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{\mathrm{3}}\geqslant\left({a}^{\mathrm{3}} {b}^{\mathrm{3}} {c}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \geqslant\mathrm{3}{abc} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\geqslant\mathrm{0} \\ $$$$\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{1}+\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\right)^{\mathrm{2}} \geqslant\mathrm{1} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{i}}\:\boldsymbol{{think}}\: \\ $$$$\mathrm{1}+\left(\boldsymbol{{a}}^{\mathrm{3}} +\boldsymbol{{b}}^{\mathrm{3}} +\boldsymbol{{c}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{{abc}}\right)^{\mathrm{2}} \geqslant\left(\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} }{{a}}\right) \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{other}}\:\boldsymbol{{check}}\:\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{correct}}\:… \\ $$
Commented by Tawa1 last updated on 13/Apr/19
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by peter frank last updated on 13/Apr/19
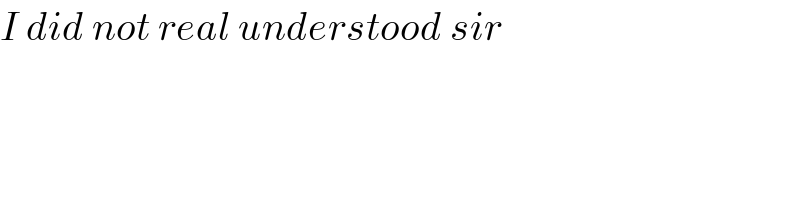
I did not real understood sir
$${I}\:{did}\:{not}\:{real}\:{understood}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *