Question Number 57864 by mr W last updated on 13/Apr/19

Answered by mr W last updated on 14/Apr/19
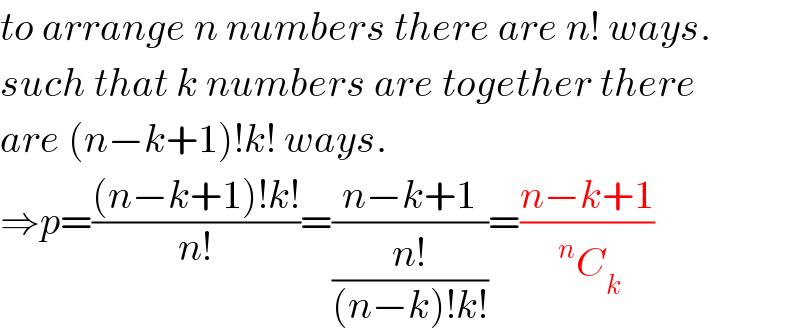
$${to}\:{arrange}\:{n}\:{numbers}\:{there}\:{are}\:{n}!\:{ways}. \\ $$$${such}\:{that}\:{k}\:{numbers}\:{are}\:{together}\:{there} \\ $$$${are}\:\left({n}−{k}+\mathrm{1}\right)!{k}!\:{ways}. \\ $$$$\Rightarrow{p}=\frac{\left({n}−{k}+\mathrm{1}\right)!{k}!}{{n}!}=\frac{{n}−{k}+\mathrm{1}}{\frac{{n}!}{\left({n}−{k}\right)!{k}!}}=\frac{{n}−{k}+\mathrm{1}}{\:^{{n}} {C}_{{k}} } \\ $$
