Question Number 57865 by mr W last updated on 13/Apr/19

Answered by MJS last updated on 13/Apr/19
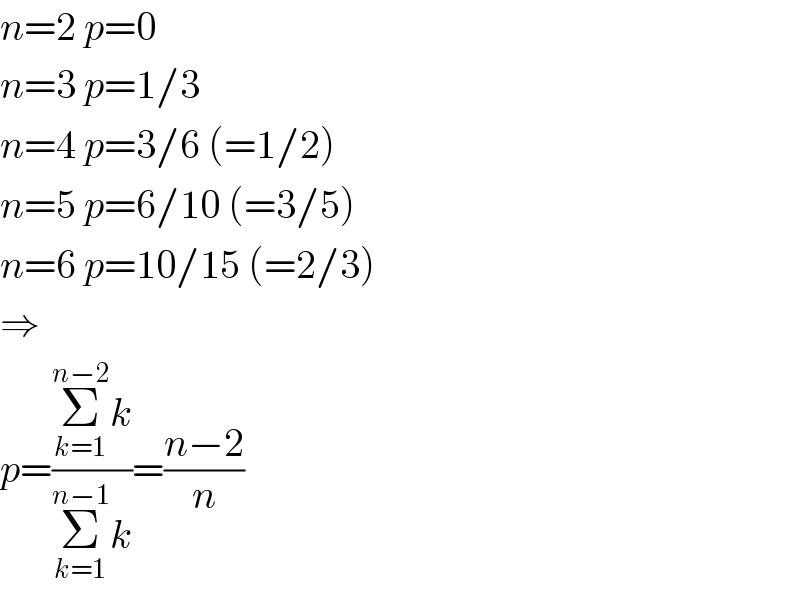
$${n}=\mathrm{2}\:{p}=\mathrm{0} \\ $$$${n}=\mathrm{3}\:{p}=\mathrm{1}/\mathrm{3} \\ $$$${n}=\mathrm{4}\:{p}=\mathrm{3}/\mathrm{6}\:\left(=\mathrm{1}/\mathrm{2}\right) \\ $$$${n}=\mathrm{5}\:{p}=\mathrm{6}/\mathrm{10}\:\left(=\mathrm{3}/\mathrm{5}\right) \\ $$$${n}=\mathrm{6}\:{p}=\mathrm{10}/\mathrm{15}\:\left(=\mathrm{2}/\mathrm{3}\right) \\ $$$$\Rightarrow \\ $$$${p}=\frac{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}{k}}{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{k}}=\frac{{n}−\mathrm{2}}{{n}} \\ $$
Commented by mr W last updated on 14/Apr/19
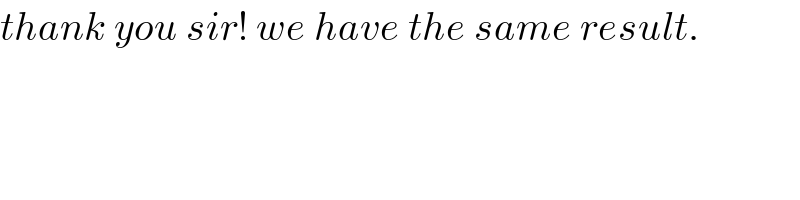
$${thank}\:{you}\:{sir}!\:{we}\:{have}\:{the}\:{same}\:{result}. \\ $$
Answered by mr W last updated on 14/Apr/19

$${to}\:{select}\:\mathrm{2}\:{from}\:{n}\:{persons}\:{there}\:{are} \\ $$$${totally}\:{C}_{\mathrm{2}} ^{{n}} =\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\:{ways}. \\ $$$${to}\:{select}\:\mathrm{2}\:{persons}\:{next}\:{to}\:{each}\:{othere} \\ $$$${there}\:{are}\:{n}−\mathrm{1}\:{ways} \\ $$$${probability}\:{to}\:{select}\:\mathrm{2}\:{persons}\:{who}\:{are} \\ $$$${together}\:{is}\:\frac{{n}−\mathrm{1}}{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}}=\frac{\mathrm{2}}{{n}} \\ $$$$\Rightarrow{probability}\:{to}\:{select}\:\mathrm{2}\:{persons}\:{who} \\ $$$${are}\:{not}\:{together}\:{is}\:{then}\:\mathrm{1}−\frac{\mathrm{2}}{{n}}=\frac{{n}−\mathrm{2}}{{n}} \\ $$
