Question Number 57915 by Tinkutara last updated on 14/Apr/19
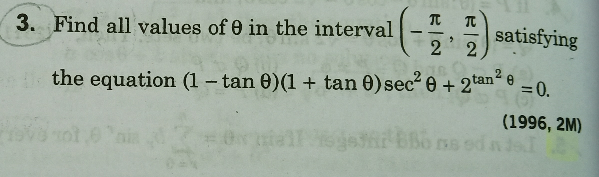
Answered by mr W last updated on 14/Apr/19
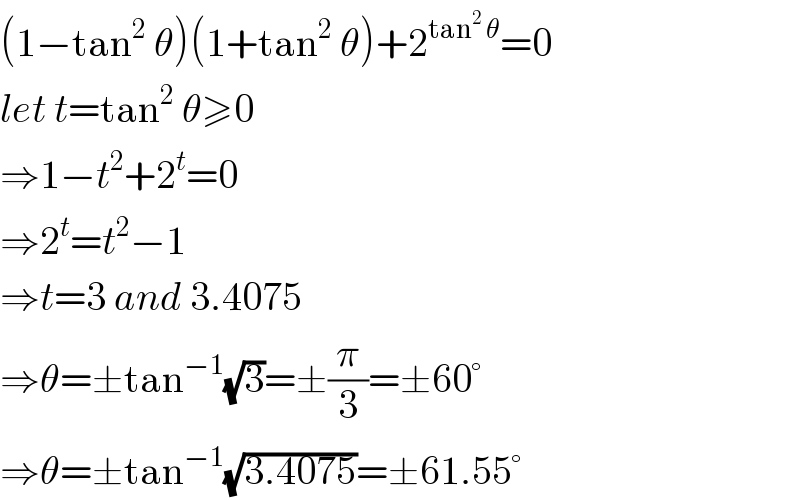
$$\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)+\mathrm{2}^{\mathrm{tan}^{\mathrm{2}} \:\theta} =\mathrm{0} \\ $$$${let}\:{t}=\mathrm{tan}^{\mathrm{2}} \:\theta\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−{t}^{\mathrm{2}} +\mathrm{2}^{{t}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}^{{t}} ={t}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow{t}=\mathrm{3}\:{and}\:\mathrm{3}.\mathrm{4075} \\ $$$$\Rightarrow\theta=\pm\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{3}}=\pm\frac{\pi}{\mathrm{3}}=\pm\mathrm{60}° \\ $$$$\Rightarrow\theta=\pm\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{3}.\mathrm{4075}}=\pm\mathrm{61}.\mathrm{55}° \\ $$
Commented by Tinkutara last updated on 14/Apr/19
t=3 can only be found with calculators?
Commented by mr W last updated on 14/Apr/19

$${t}=\mathrm{3}\:{can}\:{be}\:{found}\:{by}\:{try}.\:{other}\:{solutions} \\ $$$${can}\:{only}\:{be}\:{found}\:{through}\:{graphic} \\ $$$${tools}. \\ $$
Commented by Tinkutara last updated on 15/Apr/19
Thanks Sir!
Answered by peter frank last updated on 14/Apr/19
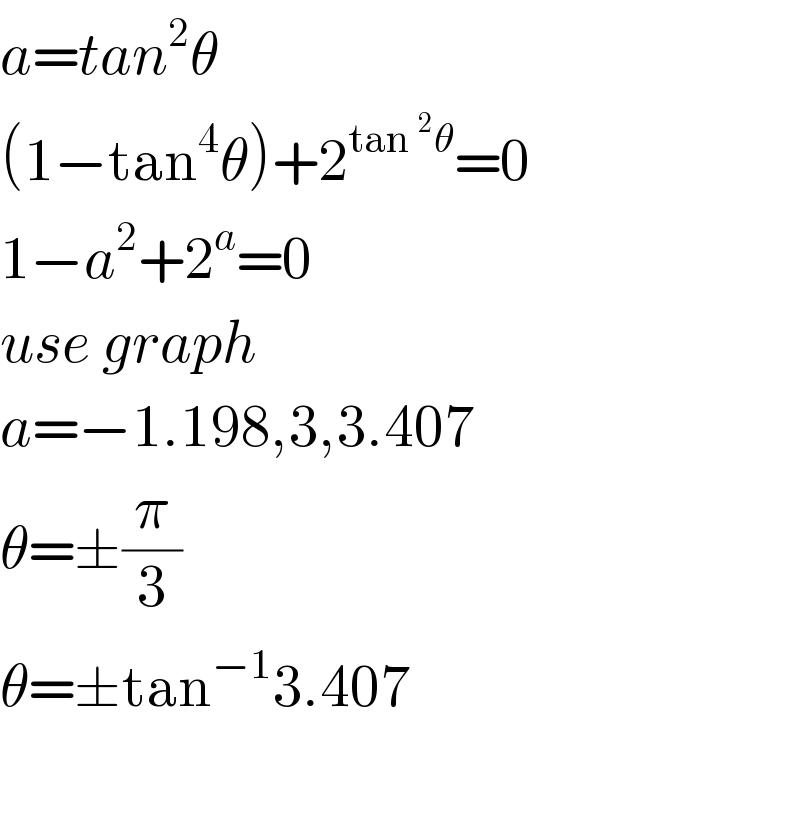
$${a}={tan}^{\mathrm{2}} \theta \\ $$$$\left(\mathrm{1}−\mathrm{tan}^{\mathrm{4}} \theta\right)+\mathrm{2}^{\mathrm{tan}\:^{\mathrm{2}} \theta} =\mathrm{0} \\ $$$$\mathrm{1}−{a}^{\mathrm{2}} +\mathrm{2}^{{a}} =\mathrm{0} \\ $$$${use}\:{graph} \\ $$$${a}=−\mathrm{1}.\mathrm{198},\mathrm{3},\mathrm{3}.\mathrm{407} \\ $$$$\theta=\pm\frac{\pi}{\mathrm{3}}\:\:\:\: \\ $$$$\theta=\pm\mathrm{tan}^{−\mathrm{1}} \mathrm{3}.\mathrm{407} \\ $$$$ \\ $$
Commented by peter frank last updated on 14/Apr/19
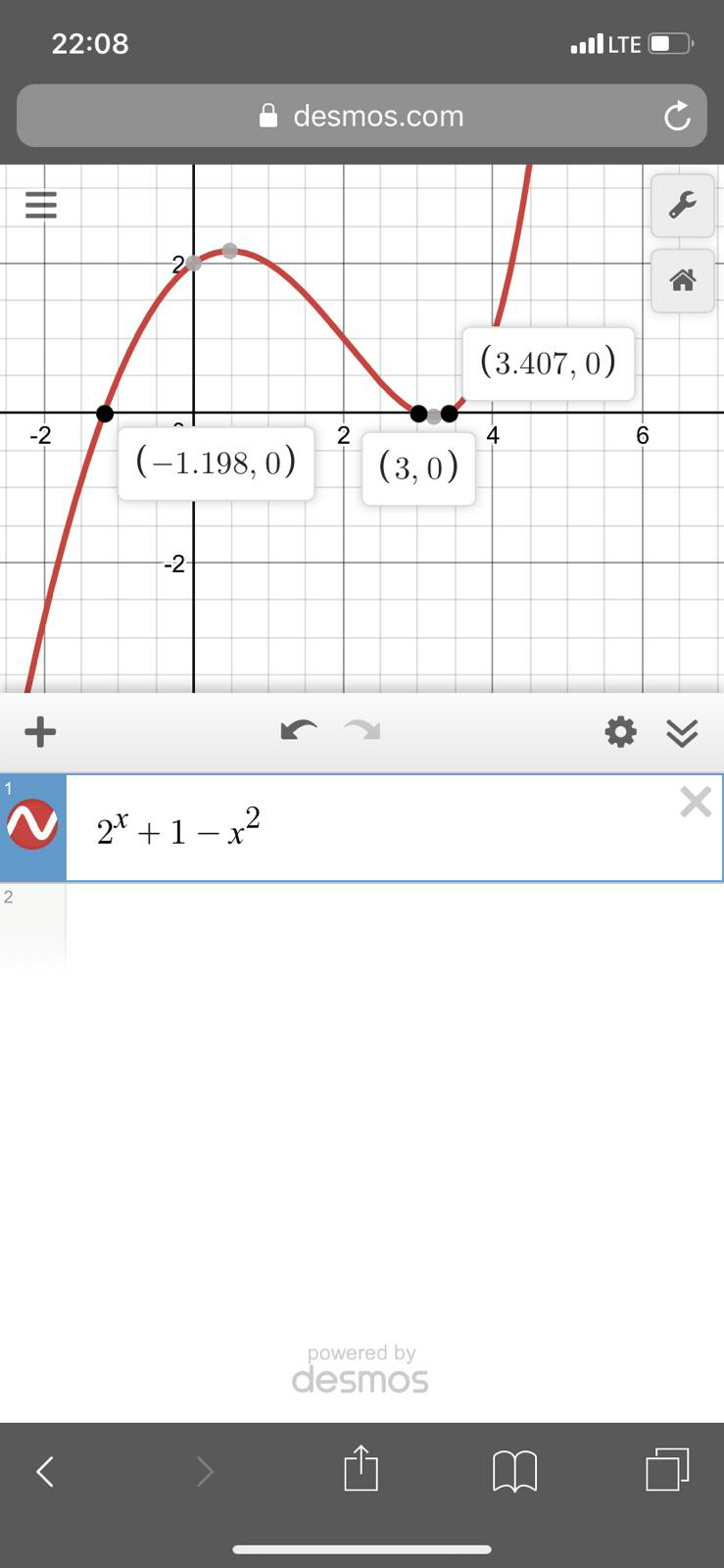
Commented by mr W last updated on 14/Apr/19
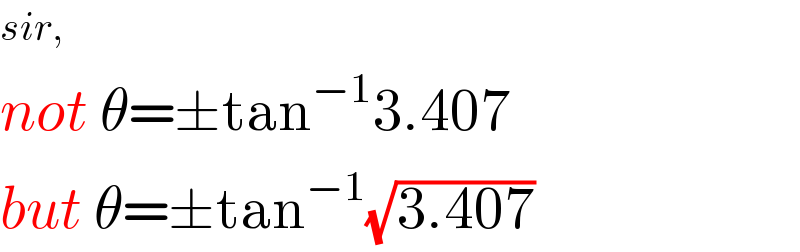
$${sir}, \\ $$$${not}\:\theta=\pm\mathrm{tan}^{−\mathrm{1}} \mathrm{3}.\mathrm{407} \\ $$$${but}\:\theta=\pm\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{3}.\mathrm{407}} \\ $$
Commented by peter frank last updated on 14/Apr/19

$${thank}\:{you} \\ $$
