Question Number 57958 by rahul 19 last updated on 15/Apr/19

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Apr/19
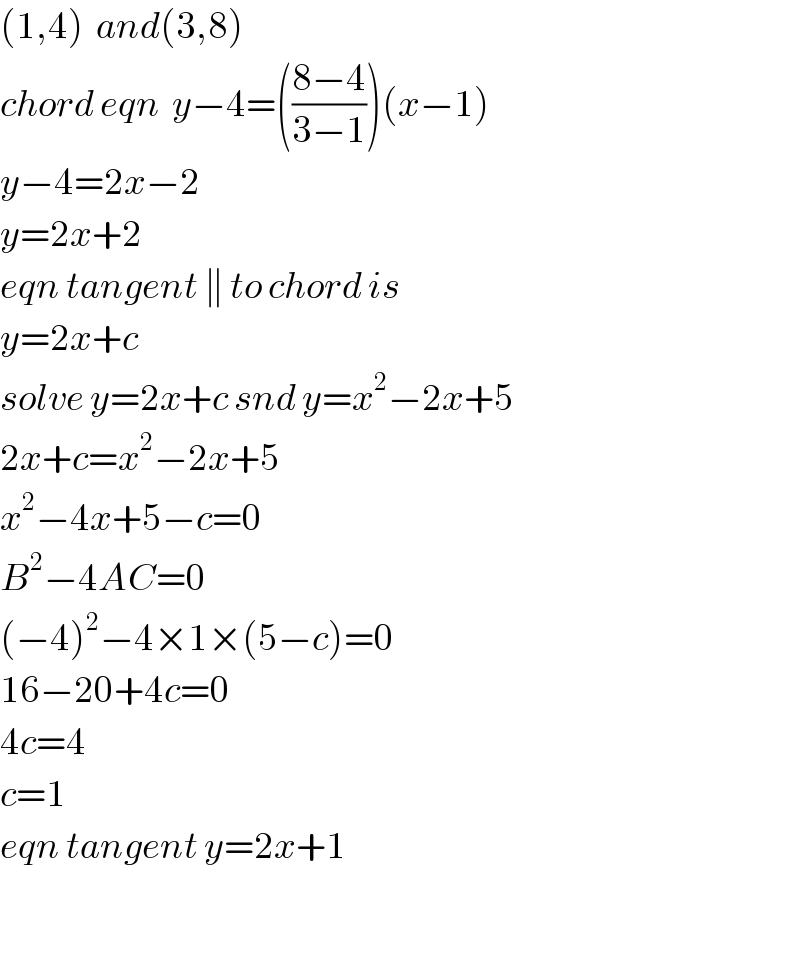
$$\left(\mathrm{1},\mathrm{4}\right)\:\:{and}\left(\mathrm{3},\mathrm{8}\right) \\ $$$${chord}\:{eqn}\:\:{y}−\mathrm{4}=\left(\frac{\mathrm{8}−\mathrm{4}}{\mathrm{3}−\mathrm{1}}\right)\left({x}−\mathrm{1}\right) \\ $$$${y}−\mathrm{4}=\mathrm{2}{x}−\mathrm{2} \\ $$$${y}=\mathrm{2}{x}+\mathrm{2} \\ $$$${eqn}\:{tangent}\:\parallel\:{to}\:{chord}\:{is} \\ $$$${y}=\mathrm{2}{x}+{c} \\ $$$${solve}\:{y}=\mathrm{2}{x}+{c}\:{snd}\:{y}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\mathrm{2}{x}+{c}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}−{c}=\mathrm{0} \\ $$$${B}^{\mathrm{2}} −\mathrm{4}{AC}=\mathrm{0} \\ $$$$\left(−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\left(\mathrm{5}−{c}\right)=\mathrm{0} \\ $$$$\mathrm{16}−\mathrm{20}+\mathrm{4}{c}=\mathrm{0} \\ $$$$\mathrm{4}{c}=\mathrm{4} \\ $$$${c}=\mathrm{1} \\ $$$${eqn}\:{tangent}\:{y}=\mathrm{2}{x}+\mathrm{1} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 15/Apr/19

$${thank}\:{you}\:{sir}. \\ $$
