Question Number 57992 by Tinkutara last updated on 15/Apr/19

Answered by MJS last updated on 16/Apr/19
![∫_1 ^c (−x^5 +8x^2 )dx=((16)/3) −(1/6)c^6 +(8/3)c^3 −(5/2)=((16)/3) c^6 −16c^3 +47=0 t=c^3 t^2 −16t+47=0 t_1 =8−(√(17)); t_2 =8+(√(17)) c_1 =((8−(√(17))))^(1/3) ; c_2 =((8+(√(17))))^(1/3) ; all other solutions ∉R but −x^5 +8x^2 =0 ⇒ x_1 =x_2 =0; x_3 =2; all other solutions ∉R ⇒ area in ]−∞; 0[ negative, in ]0; 2[ positive and in ]2; +∞[ negative c_2 ≈2.3>2 ⇒ not valid ⇒ c=c_1 =((8−(√(17))))^(1/3) c+2=2+((8−(√(17))))^(1/3) ≈3.57095](https://www.tinkutara.com/question/Q58003.png)
$$\underset{\mathrm{1}} {\overset{{c}} {\int}}\left(−{x}^{\mathrm{5}} +\mathrm{8}{x}^{\mathrm{2}} \right){dx}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}{c}^{\mathrm{6}} +\frac{\mathrm{8}}{\mathrm{3}}{c}^{\mathrm{3}} −\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$$${c}^{\mathrm{6}} −\mathrm{16}{c}^{\mathrm{3}} +\mathrm{47}=\mathrm{0} \\ $$$${t}={c}^{\mathrm{3}} \\ $$$${t}^{\mathrm{2}} −\mathrm{16}{t}+\mathrm{47}=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\mathrm{8}−\sqrt{\mathrm{17}};\:{t}_{\mathrm{2}} =\mathrm{8}+\sqrt{\mathrm{17}} \\ $$$${c}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathrm{8}−\sqrt{\mathrm{17}}};\:{c}_{\mathrm{2}} =\sqrt[{\mathrm{3}}]{\mathrm{8}+\sqrt{\mathrm{17}}};\:\mathrm{all}\:\mathrm{other}\:\mathrm{solutions}\:\notin\mathbb{R} \\ $$$$\mathrm{but} \\ $$$$−{x}^{\mathrm{5}} +\mathrm{8}{x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{x}_{\mathrm{1}} ={x}_{\mathrm{2}} =\mathrm{0};\:{x}_{\mathrm{3}} =\mathrm{2};\:\mathrm{all}\:\mathrm{other}\:\mathrm{solutions}\:\notin\mathbb{R} \\ $$$$\left.\Rightarrow\:\mathrm{area}\:\mathrm{in}\:\right]−\infty;\:\mathrm{0}\left[\:\mathrm{negative},\:\mathrm{in}\:\right]\mathrm{0};\:\mathrm{2}\left[\:\mathrm{positive}\right. \\ $$$$\left.\:\:\:\:\:\:\mathrm{and}\:\mathrm{in}\:\right]\mathrm{2};\:+\infty\left[\:\mathrm{negative}\right. \\ $$$${c}_{\mathrm{2}} \approx\mathrm{2}.\mathrm{3}>\mathrm{2}\:\Rightarrow\:\mathrm{not}\:\mathrm{valid} \\ $$$$\Rightarrow\:{c}={c}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathrm{8}−\sqrt{\mathrm{17}}} \\ $$$${c}+\mathrm{2}=\mathrm{2}+\sqrt[{\mathrm{3}}]{\mathrm{8}−\sqrt{\mathrm{17}}}\approx\mathrm{3}.\mathrm{57095} \\ $$
Commented by MJS last updated on 16/Apr/19
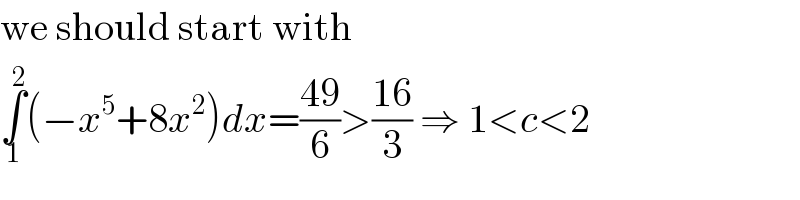
$$\mathrm{we}\:\mathrm{should}\:\mathrm{start}\:\mathrm{with} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\left(−{x}^{\mathrm{5}} +\mathrm{8}{x}^{\mathrm{2}} \right){dx}=\frac{\mathrm{49}}{\mathrm{6}}>\frac{\mathrm{16}}{\mathrm{3}}\:\Rightarrow\:\mathrm{1}<{c}<\mathrm{2} \\ $$
Commented by Tinkutara last updated on 18/Apr/19
Thanks Sir! Maybe the answer 1 in book is wrong.
