Question Number 58001 by rahul 19 last updated on 16/Apr/19

Commented by rahul 19 last updated on 16/Apr/19
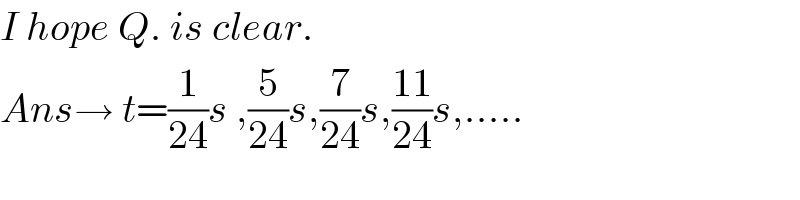
$${I}\:{hope}\:{Q}.\:{is}\:{clear}. \\ $$$${Ans}\rightarrow\:{t}=\frac{\mathrm{1}}{\mathrm{24}}{s}\:,\frac{\mathrm{5}}{\mathrm{24}}{s},\frac{\mathrm{7}}{\mathrm{24}}{s},\frac{\mathrm{11}}{\mathrm{24}}{s},….. \\ $$
Answered by mr W last updated on 16/Apr/19
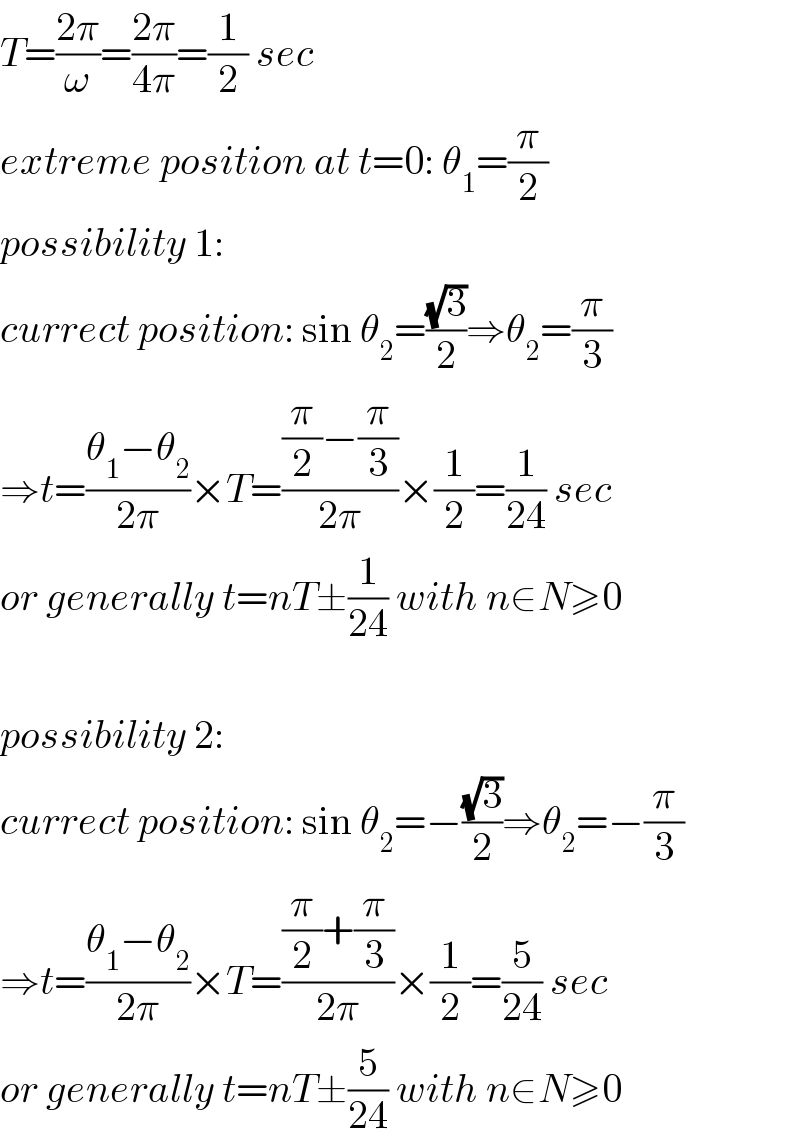
$${T}=\frac{\mathrm{2}\pi}{\omega}=\frac{\mathrm{2}\pi}{\mathrm{4}\pi}=\frac{\mathrm{1}}{\mathrm{2}}\:{sec} \\ $$$${extreme}\:{position}\:{at}\:{t}=\mathrm{0}:\:\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{2}} \\ $$$${possibility}\:\mathrm{1}: \\ $$$${currect}\:{position}:\:\mathrm{sin}\:\theta_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow{t}=\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}\pi}×{T}=\frac{\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}}{\mathrm{2}\pi}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{24}}\:{sec} \\ $$$${or}\:{generally}\:{t}={nT}\pm\frac{\mathrm{1}}{\mathrm{24}}\:{with}\:{n}\in{N}\geqslant\mathrm{0} \\ $$$$ \\ $$$${possibility}\:\mathrm{2}: \\ $$$${currect}\:{position}:\:\mathrm{sin}\:\theta_{\mathrm{2}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow\theta_{\mathrm{2}} =−\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow{t}=\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}\pi}×{T}=\frac{\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}}{\mathrm{2}\pi}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{24}}\:{sec} \\ $$$${or}\:{generally}\:{t}={nT}\pm\frac{\mathrm{5}}{\mathrm{24}}\:{with}\:{n}\in{N}\geqslant\mathrm{0} \\ $$
Commented by rahul 19 last updated on 16/Apr/19
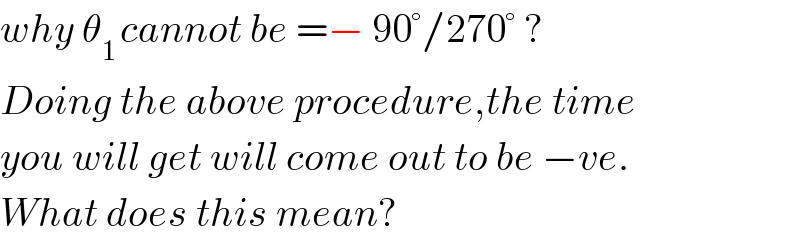
$${why}\:\theta_{\mathrm{1}\:} {cannot}\:{be}\:=−\:\mathrm{90}°/\mathrm{270}°\:? \\ $$$${Doing}\:{the}\:{above}\:{procedure},{the}\:{time} \\ $$$${you}\:{will}\:{get}\:{will}\:{come}\:{out}\:{to}\:{be}\:−{ve}. \\ $$$${What}\:{does}\:{this}\:{mean}? \\ $$
Commented by mr W last updated on 16/Apr/19
Commented by mr W last updated on 16/Apr/19

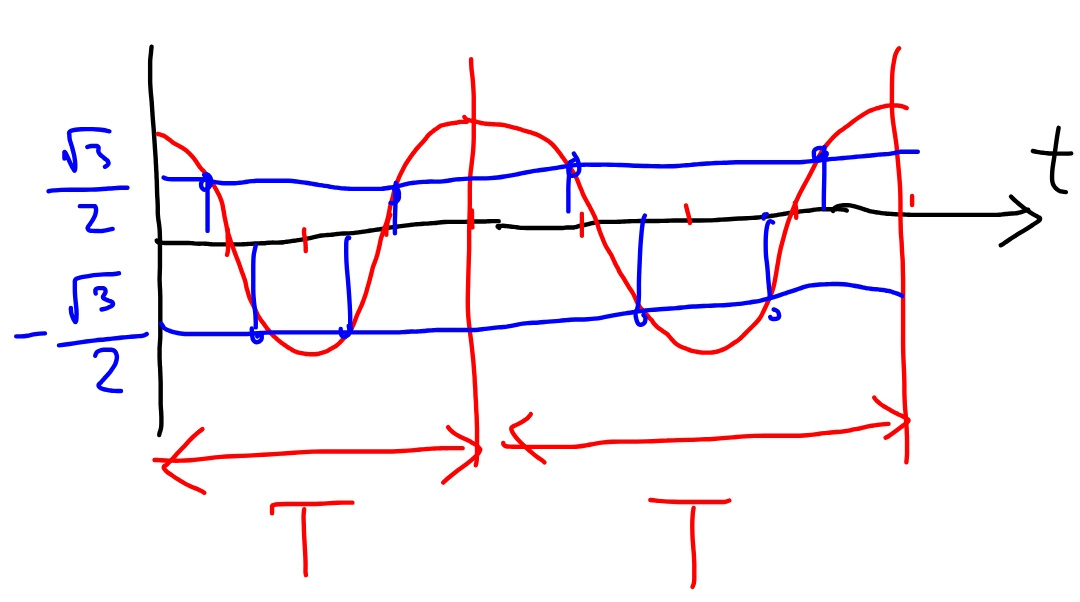
$$\theta_{\mathrm{1}} \:{can}\:{be}\:{taken}\:{as}\:{any}\:{value}.\:{we}\:{are}\:{only} \\ $$$${interested}\:{at}\:\theta_{\mathrm{1}} −\theta_{\mathrm{2}} . \\ $$$${you}\:{understand}\:{what}\:{is}\:{meant}\:{with} \\ $$$${t}={nT}\pm\frac{\mathrm{1}}{\mathrm{24}}\:{and}\:{t}={nT}\pm\frac{\mathrm{5}}{\mathrm{24}}.\:{in}\:{each} \\ $$$${periode}\:{T}\:{there}\:{arefour}\:{instants}\:{at}\:{which} \\ $$$${the}\:{position}\:{is}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{apart}\:{from}\:{the}\:{mean} \\ $$$${position}\:{as}\:{shown}\:{in}\:{the}\:{diagram}. \\ $$$${t}\:{is}\:{certainly}\:>\mathrm{0}.\:{naturally}\:{i}\:{can}\:{write} \\ $$$${t}={nT}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${t}={nT}+\frac{\mathrm{5}}{\mathrm{24}} \\ $$$${t}={nT}+\frac{\mathrm{7}}{\mathrm{24}} \\ $$$${t}={nT}+\frac{\mathrm{11}}{\mathrm{24}} \\ $$
Commented by rahul 19 last updated on 16/Apr/19

$${thank}\:{you}\:{sir}. \\ $$
