Menu Close

Question-58067

Tinku Tara 0 Comments
Pin




Question Number 58067 by mustakim420 last updated on 17/Apr/19
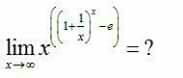
Commented by maxmathsup by imad last updated on 17/Apr/19
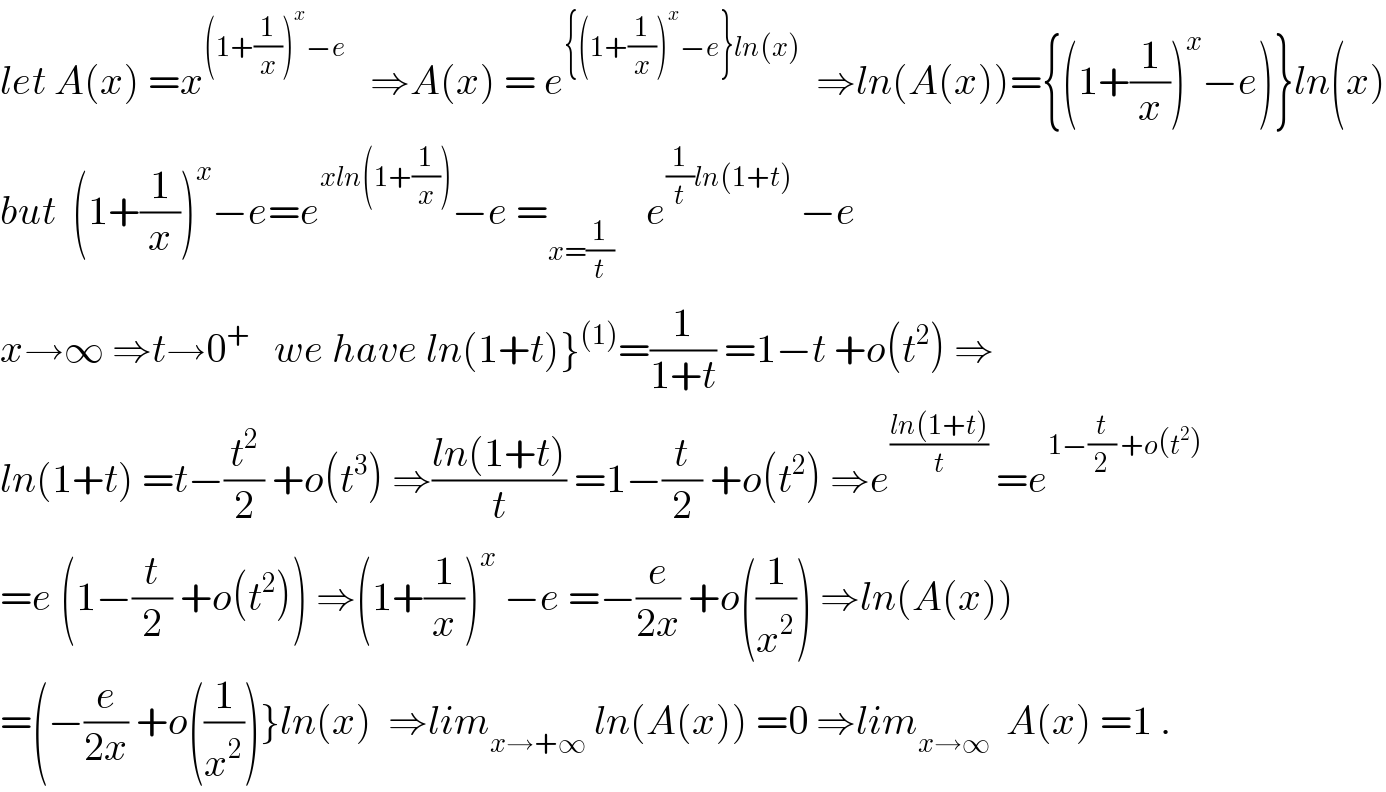
let A(x) =x^((1+(1/x))^x −e) ⇒A(x) = e^({(1+(1/x))^x −e}ln(x)) ⇒ln(A(x))={(1+(1/x))^x −e)}ln(x) but (1+(1/x))^x −e=e^(xln(1+(1/x))) −e =_(x=(1/t)) e^((1/t)ln(1+t)) −e x→∞ ⇒t→0^+ we have ln(1+t)}^((1)) =(1/(1+t)) =1−t +o(t^2 ) ⇒ ln(1+t) =t−(t^2 /2) +o(t^3 ) ⇒((ln(1+t))/t) =1−(t/2) +o(t^2 ) ⇒e^((ln(1+t))/t) =e^(1−(t/2) +o(t^2 )) =e (1−(t/2) +o(t^2 )) ⇒(1+(1/x))^x −e =−(e/(2x)) +o((1/x^2 )) ⇒ln(A(x)) =(−(e/(2x)) +o((1/x^2 ))}ln(x) ⇒lim_(x→+∞) ln(A(x)) =0 ⇒lim_(x→∞) A(x) =1 .
$$\left.{let}\:{A}\left({x}\right)\:={x}^{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} −{e}} \:\:\:\Rightarrow{A}\left({x}\right)\:=\:{e}^{\left\{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} −{e}\right\}{ln}\left({x}\right)} \:\:\Rightarrow{ln}\left({A}\left({x}\right)\right)=\left\{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} −{e}\right)\right\}{ln}\left({x}\right) \\ $$$${but}\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} −{e}={e}^{{xln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} −{e}\:=_{{x}=\frac{\mathrm{1}}{{t}}} \:\:\:\:{e}^{\frac{\mathrm{1}}{{t}}{ln}\left(\mathrm{1}+{t}\right)} \:−{e} \\ $$$$\left.{x}\rightarrow\infty\:\Rightarrow{t}\rightarrow\mathrm{0}^{+} \:\:\:{we}\:{have}\:{ln}\left(\mathrm{1}+{t}\right)\right\}^{\left(\mathrm{1}\right)} =\frac{\mathrm{1}}{\mathrm{1}+{t}}\:=\mathrm{1}−{t}\:+{o}\left({t}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}\right)\:={t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({t}^{\mathrm{3}} \right)\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}\:=\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+{o}\left({t}^{\mathrm{2}} \right)\:\Rightarrow{e}^{\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}} \:={e}^{\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+{o}\left({t}^{\mathrm{2}} \right)} \: \\ $$$$={e}\:\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+{o}\left({t}^{\mathrm{2}} \right)\right)\:\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} \:−{e}\:=−\frac{{e}}{\mathrm{2}{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow{ln}\left({A}\left({x}\right)\right) \\ $$$$=\left(−\frac{{e}}{\mathrm{2}{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right\}{ln}\left({x}\right)\:\:\Rightarrow{lim}_{{x}\rightarrow+\infty} \:{ln}\left({A}\left({x}\right)\right)\:=\mathrm{0}\:\Rightarrow{lim}_{{x}\rightarrow\infty} \:\:{A}\left({x}\right)\:=\mathrm{1}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *