Question Number 58132 by ajfour last updated on 18/Apr/19
Commented by ajfour last updated on 18/Apr/19
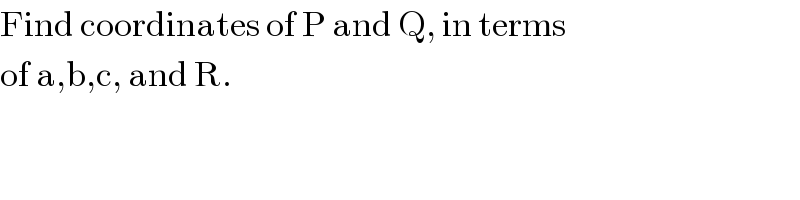
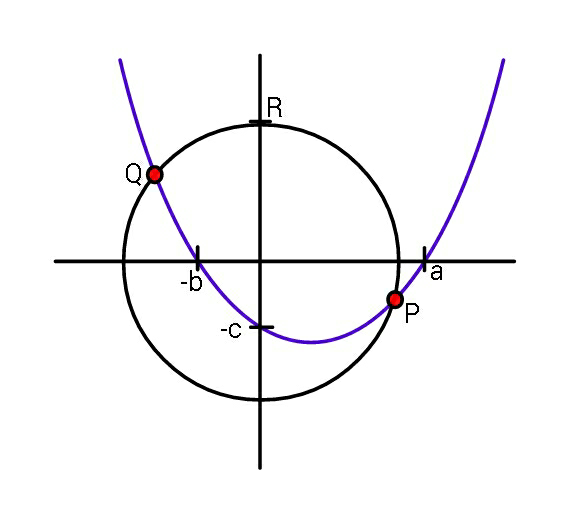
$$\mathrm{Find}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{P}\:\mathrm{and}\:\mathrm{Q},\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{a},\mathrm{b},\mathrm{c},\:\mathrm{and}\:\mathrm{R}. \\ $$
Answered by tanmay last updated on 18/Apr/19
![parabola y=αx^2 +βx+γ 0=αa^2 +βa+γ 0=αb^2 +β(−b)+γ −c=α×0^2 +β×0^2 +γ [ γ=−c] y=αx^2 +βx−c αa^2 +βa=αb^2 −βb α(a+b)(a−b)+β(a+b)=0 α(a−b)+β=0 β=α(b−a) 0=αa^2 +βa+γ 0=αa^2 +αa(b−a)−c c=α(a^2 +ab−a^2 ) α=(c/(ab)) β=(c/(ab))(b−a) parabola eqn y=((c/(ab)))x^2 +(c/(ab))(b−a)x−c←chek it again R+c=a+b radius ofcircle=a+b−c eqn of circle x^2 +y^2 =(a+b−c)^2 ←check it pls check eqn of circle and parabola... if correct...then to solve to find P and Q](https://www.tinkutara.com/question/Q58141.png)
$$ \\ $$$${parabola}\:{y}=\alpha{x}^{\mathrm{2}} +\beta{x}+\gamma \\ $$$$\mathrm{0}=\alpha{a}^{\mathrm{2}} +\beta{a}+\gamma \\ $$$$\mathrm{0}=\alpha{b}^{\mathrm{2}} +\beta\left(−{b}\right)+\gamma \\ $$$$−{c}=\alpha×\mathrm{0}^{\mathrm{2}} +\beta×\mathrm{0}^{\mathrm{2}} +\gamma\:\:\:\:\left[\:\gamma=−{c}\right] \\ $$$${y}=\alpha{x}^{\mathrm{2}} +\beta{x}−{c} \\ $$$$\alpha{a}^{\mathrm{2}} +\beta{a}=\alpha{b}^{\mathrm{2}} −\beta{b} \\ $$$$\alpha\left({a}+{b}\right)\left({a}−{b}\right)+\beta\left({a}+{b}\right)=\mathrm{0} \\ $$$$\alpha\left({a}−{b}\right)+\beta=\mathrm{0} \\ $$$$\beta=\alpha\left({b}−{a}\right) \\ $$$$\mathrm{0}=\alpha{a}^{\mathrm{2}} +\beta{a}+\gamma \\ $$$$\mathrm{0}=\alpha{a}^{\mathrm{2}} +\alpha{a}\left({b}−{a}\right)−{c} \\ $$$${c}=\alpha\left({a}^{\mathrm{2}} +{ab}−{a}^{\mathrm{2}} \right) \\ $$$$\alpha=\frac{{c}}{{ab}}\:\:\:\beta=\frac{{c}}{{ab}}\left({b}−{a}\right) \\ $$$${parabola}\:{eqn}\:\:{y}=\left(\frac{{c}}{{ab}}\right){x}^{\mathrm{2}} +\frac{{c}}{{ab}}\left({b}−{a}\right){x}−{c}\leftarrow{chek}\:{it} \\ $$$${again}\:\:{R}+{c}={a}+{b} \\ $$$${radius}\:{ofcircle}={a}+{b}−{c} \\ $$$${eqn}\:{of}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({a}+{b}−{c}\right)^{\mathrm{2}} \leftarrow{check}\:{it} \\ $$$${pls}\:{check}\:{eqn}\:{of}\:{circle}\:{and}\:{parabola}… \\ $$$${if}\:{correct}…{then}\:{to}\:{solve}\:{to}\:{find}\:{P}\:{and}\:{Q} \\ $$
Commented by 121194 last updated on 18/Apr/19

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \left(\mathrm{no}\:\mathrm{relation}\right) \\ $$
Commented by tanmay last updated on 18/Apr/19
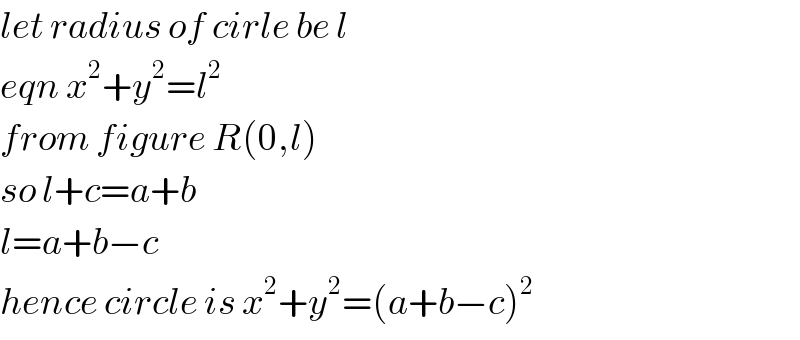
$${let}\:{radius}\:{of}\:{cirle}\:{be}\:{l} \\ $$$${eqn}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={l}^{\mathrm{2}} \\ $$$${from}\:{figure}\:{R}\left(\mathrm{0},{l}\right) \\ $$$${so}\:{l}+{c}={a}+{b} \\ $$$${l}={a}+{b}−{c} \\ $$$${hence}\:{circle}\:{is}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({a}+{b}−{c}\right)^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 18/Apr/19

$$\mathrm{never}\:\mathrm{mind}\:\mathrm{Sir},\:\mathrm{it}\:\mathrm{would}\:\mathrm{of}\:\mathrm{course} \\ $$$$\mathrm{land}\:\mathrm{on}\:\mathrm{solving}\:\mathrm{a}\:\mathrm{general}\:\mathrm{biquadratric}, \\ $$$$\mathrm{i}\:\mathrm{understand}..\mathrm{have}\:\mathrm{gotten}\:\mathrm{bit}\:\mathrm{busy} \\ $$$$\mathrm{these}\:\mathrm{days},\:\mathrm{shall}\:\mathrm{post}\:\mathrm{a}\:\mathrm{good}\:\mathrm{question} \\ $$$$\mathrm{soon}. \\ $$
Answered by mr W last updated on 18/Apr/19
![eqn. of parabola: y=α(x−((a+b)/2))^2 +β 0=α(a−((a+b)/2))^2 +β ⇒0=α(((a−b)/2))^2 +β ..(i) c=α(0−((a+b)/2))^2 +β ⇒c=α(((a+b)/2))^2 +β ..(ii) (ii)−(i): αab=c ⇒α=(c/(ab)) ⇒β=−((c(a−b)^2 )/(4ab)) let P,Q=(u,v) v=α(u−((a+b)/2))^2 +β ...(iv) u^2 +v^2 =R^2 u^2 +[α(u−((a+b)/2))^2 +β]^2 =R^2 ⇒u^2 +[(c/(ab))(u−((a+b)/2))^2 −((c(a−b)^2 )/(4ab))]^2 =R^2 ⇒u^2 +((c/(ab)))^2 (u−a)^2 (u−b)^2 =R^2 ...(iii) from (iii) u=f(a,b,c,R)=....... (iii) may have no solution, one solution, two, three or four solutions.](https://www.tinkutara.com/question/Q58151.png)
$${eqn}.\:{of}\:{parabola}: \\ $$$${y}=\alpha\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta \\ $$$$\mathrm{0}=\alpha\left({a}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta \\ $$$$\Rightarrow\mathrm{0}=\alpha\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta\:\:\:..\left({i}\right) \\ $$$${c}=\alpha\left(\mathrm{0}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta \\ $$$$\Rightarrow{c}=\alpha\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta\:\:\:..\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\alpha{ab}={c} \\ $$$$\Rightarrow\alpha=\frac{{c}}{{ab}} \\ $$$$\Rightarrow\beta=−\frac{{c}\left({a}−{b}\right)^{\mathrm{2}} }{\mathrm{4}{ab}} \\ $$$${let}\:{P},{Q}=\left({u},{v}\right) \\ $$$${v}=\alpha\left({u}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta\:\:\:\:…\left({iv}\right) \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} +\left[\alpha\left({u}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\beta\right]^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +\left[\frac{{c}}{{ab}}\left({u}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{{c}\left({a}−{b}\right)^{\mathrm{2}} }{\mathrm{4}{ab}}\right]^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +\left(\frac{{c}}{{ab}}\right)^{\mathrm{2}} \left({u}−{a}\right)^{\mathrm{2}} \left({u}−{b}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${from}\:\left({iii}\right)\:{u}={f}\left({a},{b},{c},{R}\right)=……. \\ $$$$\left({iii}\right)\:{may}\:{have}\:{no}\:{solution},\:{one}\:{solution}, \\ $$$${two},\:{three}\:{or}\:{four}\:{solutions}. \\ $$
Commented by ajfour last updated on 20/Apr/19

$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{i}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{arrive} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{final}\:\mathrm{eq}.\:\mathrm{even}\:\mathrm{in}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{manner}: \\ $$$$\:\:\mathrm{y}=\mathrm{A}\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}−\mathrm{b}\right) \\ $$$$\&\:\mathrm{since}\:\:\:−\mathrm{c}=\mathrm{Aab}\:\:\Rightarrow\:\:\mathrm{A}=−\frac{\mathrm{c}}{\mathrm{ab}} \\ $$$$\mathrm{so}\:\:\:\mathrm{y}=−\frac{\mathrm{c}}{\mathrm{ab}}\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}−\mathrm{b}\right) \\ $$$$\mathrm{and}\:\mathrm{circle}\:\mathrm{eq}.\:\mathrm{is}\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \\ $$$$\mathrm{hence} \\ $$$$\:\:\:\:\:\:\:\mathrm{for}\:\mathrm{x}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{intersection} \\ $$$$\mathrm{points} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\left(\frac{\mathrm{c}}{\mathrm{ab}}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{a}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{b}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \:\:. \\ $$
Commented by mr W last updated on 20/Apr/19

$${very}\:{smart}\:{sir}! \\ $$
