Question-58512

Question Number 58512 by ajfour last updated on 24/Apr/19

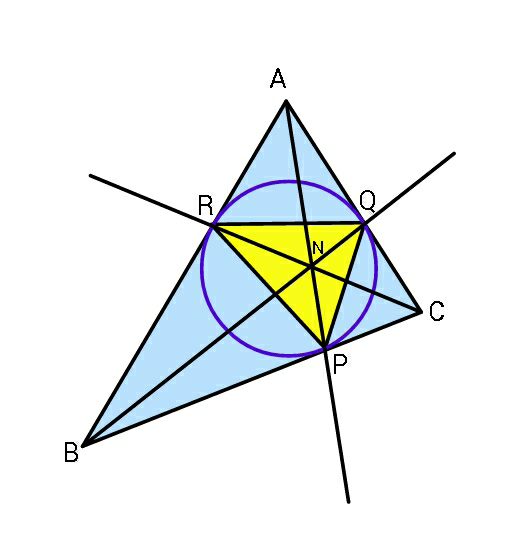
Commented by ajfour last updated on 24/Apr/19

Find ((Area(△PQR))/(Area(△ABC))) in terms of a,b,c.

$$\mathrm{Find}\:\:\:\:\:\frac{\mathrm{Area}\left(\bigtriangleup\mathrm{PQR}\right)}{\mathrm{Area}\left(\bigtriangleup\mathrm{ABC}\right)}\:\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c}. \\ $$

Answered by mr W last updated on 24/Apr/19

let α=AR=AQ β=BP=BR γ=CP=CQ we have β+γ=a γ+α=b α+β=c ⇒α+β+γ=((a+b+c)/2)=s ⇒α=s−a=((−a+b+c)/2) ⇒β=s−b=((a−b+c)/2) ⇒γ=s−c=((a+b−c)/2) Δ_(ARQ) =((α^2 sin A)/2)=(α^2 /(bc))×((bc sin A)/2)=(α^2 /(bc))Δ_(ABC) =a(−a+b+c)^2 ×(Δ_(ABC) /(4abc)) similarly: Δ_(BPR) =b(a−b+c)^2 ×(Δ_(ABC) /(4abc)) Δ_(CQP) =c(a+b−c)^2 ×(Δ_(ABC) /(4abc)) Δ_(PQR) =Δ_(ABC) −{a(−a+b+c)^2 +b(a−b+c)^2 +c(a+b−c)^2 }×(Δ_(ABC) /(4abc)) Δ_(PQR) =Δ_(ABC) −{a(a+b+c−2a)^2 +b(a+b+c−2b)^2 +c(a+b+c−2c)^2 }×(Δ_(ABC) /(4abc)) Δ_(PQR) =Δ_(ABC) −{(a+b+c)^3 −4(a^2 +b^2 +c^2 )(a+b+c)+4(a^3 +b^3 +c^3 )}×(Δ_(ABC) /(4abc)) ⇒(Δ_(PQR) /Δ_(ABC) )=1−(((a+b+c)^3 −4(a^2 +b^2 +c^2 )(a+b+c)+4(a^3 +b^3 +c^3 ))/(4abc)) if a=b=c: (Δ_(PQR) /Δ_(ABC) )=1−((3^3 −4×3×3+4×3)/4)=1−(3/4)=(1/4)

$${let} \\ $$$$\alpha={AR}={AQ} \\ $$$$\beta={BP}={BR} \\ $$$$\gamma={CP}={CQ} \\ $$$${we}\:{have} \\ $$$$\beta+\gamma={a} \\ $$$$\gamma+\alpha={b} \\ $$$$\alpha+\beta={c} \\ $$$$\Rightarrow\alpha+\beta+\gamma=\frac{{a}+{b}+{c}}{\mathrm{2}}={s} \\ $$$$\Rightarrow\alpha={s}−{a}=\frac{−{a}+{b}+{c}}{\mathrm{2}} \\ $$$$\Rightarrow\beta={s}−{b}=\frac{{a}−{b}+{c}}{\mathrm{2}} \\ $$$$\Rightarrow\gamma={s}−{c}=\frac{{a}+{b}−{c}}{\mathrm{2}} \\ $$$$\Delta_{{ARQ}} =\frac{\alpha^{\mathrm{2}} \:\mathrm{sin}\:{A}}{\mathrm{2}}=\frac{\alpha^{\mathrm{2}} }{{bc}}×\frac{{bc}\:\mathrm{sin}\:{A}}{\mathrm{2}}=\frac{\alpha^{\mathrm{2}} }{{bc}}\Delta_{{ABC}} ={a}\left(−{a}+{b}+{c}\right)^{\mathrm{2}} ×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$${similarly}: \\ $$$$\Delta_{{BPR}} ={b}\left({a}−{b}+{c}\right)^{\mathrm{2}} ×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$$\Delta_{{CQP}} ={c}\left({a}+{b}−{c}\right)^{\mathrm{2}} ×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$$\Delta_{{PQR}} =\Delta_{{ABC}} −\left\{{a}\left(−{a}+{b}+{c}\right)^{\mathrm{2}} +{b}\left({a}−{b}+{c}\right)^{\mathrm{2}} +{c}\left({a}+{b}−{c}\right)^{\mathrm{2}} \right\}×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$$\Delta_{{PQR}} =\Delta_{{ABC}} −\left\{{a}\left({a}+{b}+{c}−\mathrm{2}{a}\right)^{\mathrm{2}} +{b}\left({a}+{b}+{c}−\mathrm{2}{b}\right)^{\mathrm{2}} +{c}\left({a}+{b}+{c}−\mathrm{2}{c}\right)^{\mathrm{2}} \right\}×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$$\Delta_{{PQR}} =\Delta_{{ABC}} −\left\{\left({a}+{b}+{c}\right)^{\mathrm{3}} −\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}+{b}+{c}\right)+\mathrm{4}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)\right\}×\frac{\Delta_{{ABC}} }{\mathrm{4}{abc}} \\ $$$$\Rightarrow\frac{\Delta_{{PQR}} }{\Delta_{{ABC}} }=\mathrm{1}−\frac{\left({a}+{b}+{c}\right)^{\mathrm{3}} −\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}+{b}+{c}\right)+\mathrm{4}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)}{\mathrm{4}{abc}} \\ $$$$ \\ $$$${if}\:{a}={b}={c}: \\ $$$$\frac{\Delta_{{PQR}} }{\Delta_{{ABC}} }=\mathrm{1}−\frac{\mathrm{3}^{\mathrm{3}} −\mathrm{4}×\mathrm{3}×\mathrm{3}+\mathrm{4}×\mathrm{3}}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by ajfour last updated on 25/Apr/19

Thank you Sir,excellent! Sir. I m busy teaching class 8−12 in a school and mis my time with the forum; those were the days my Sir, i thought they′d never end..

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir},\mathrm{excellent}!\:\mathrm{Sir}. \\ $$$$\mathrm{I}\:\mathrm{m}\:\mathrm{busy}\:\mathrm{teaching}\:\mathrm{class}\:\mathrm{8}−\mathrm{12}\:\mathrm{in}\:\mathrm{a} \\ $$$$\mathrm{school}\:\mathrm{and}\:\mathrm{mis}\:\mathrm{my}\:\mathrm{time}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{forum};\:\mathrm{those}\:\mathrm{were}\:\mathrm{the}\:\mathrm{days}\:\mathrm{my}\:\mathrm{Sir}, \\ $$$$\mathrm{i}\:\mathrm{thought}\:\mathrm{they}'\mathrm{d}\:\mathrm{never}\:\mathrm{end}.. \\ $$

Commented by mr W last updated on 26/Apr/19

$${dear}\:{sir}:\:{i}\:{can}\:{understand}\:{you}\:{very} \\ $$$${well}.\:{the}\:{real}\:{life}\:{is}\:{outside}\:{off}\:{the} \\ $$$${forum},\:{it}'{s}\:{more}\:{important}!\:{i}\:{wish} \\ $$$${you}\:{all}\:{the}\:{best}\:{in}\:{it}.\:{when}\:{you}\:{find} \\ $$$${time},\:{just}\:{come}\:{back}\:{and}\:{let}\:{us}\:{admire}\: \\ $$$${your}\:{questions}\:{and}\:{answers}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply