Question Number 58547 by naka3546 last updated on 24/Apr/19

Commented by naka3546 last updated on 24/Apr/19
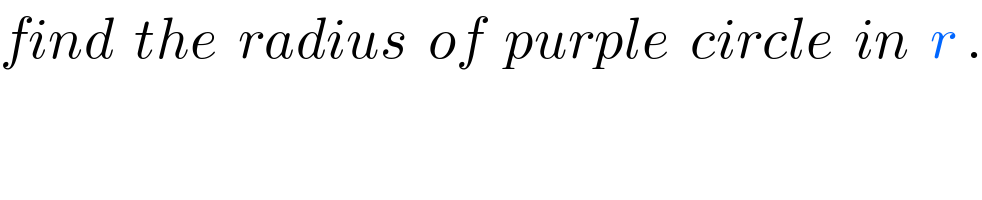
$${find}\:\:{the}\:\:{radius}\:\:{of}\:\:{purple}\:\:{circle}\:\:{in}\:\:{r}\:. \\ $$
Answered by mr W last updated on 24/Apr/19

Commented by mr W last updated on 24/Apr/19
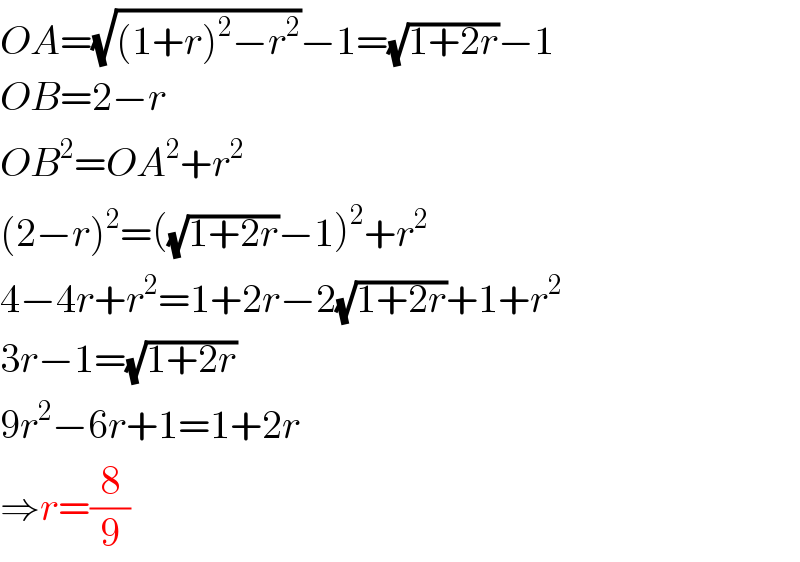
$${OA}=\sqrt{\left(\mathrm{1}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }−\mathrm{1}=\sqrt{\mathrm{1}+\mathrm{2}{r}}−\mathrm{1} \\ $$$${OB}=\mathrm{2}−{r} \\ $$$${OB}^{\mathrm{2}} ={OA}^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}−{r}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{1}+\mathrm{2}{r}}−\mathrm{1}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\mathrm{4}−\mathrm{4}{r}+{r}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{r}−\mathrm{2}\sqrt{\mathrm{1}+\mathrm{2}{r}}+\mathrm{1}+{r}^{\mathrm{2}} \\ $$$$\mathrm{3}{r}−\mathrm{1}=\sqrt{\mathrm{1}+\mathrm{2}{r}} \\ $$$$\mathrm{9}{r}^{\mathrm{2}} −\mathrm{6}{r}+\mathrm{1}=\mathrm{1}+\mathrm{2}{r} \\ $$$$\Rightarrow{r}=\frac{\mathrm{8}}{\mathrm{9}} \\ $$
