Question Number 58595 by rahul 19 last updated on 25/Apr/19

Answered by tanmay last updated on 26/Apr/19
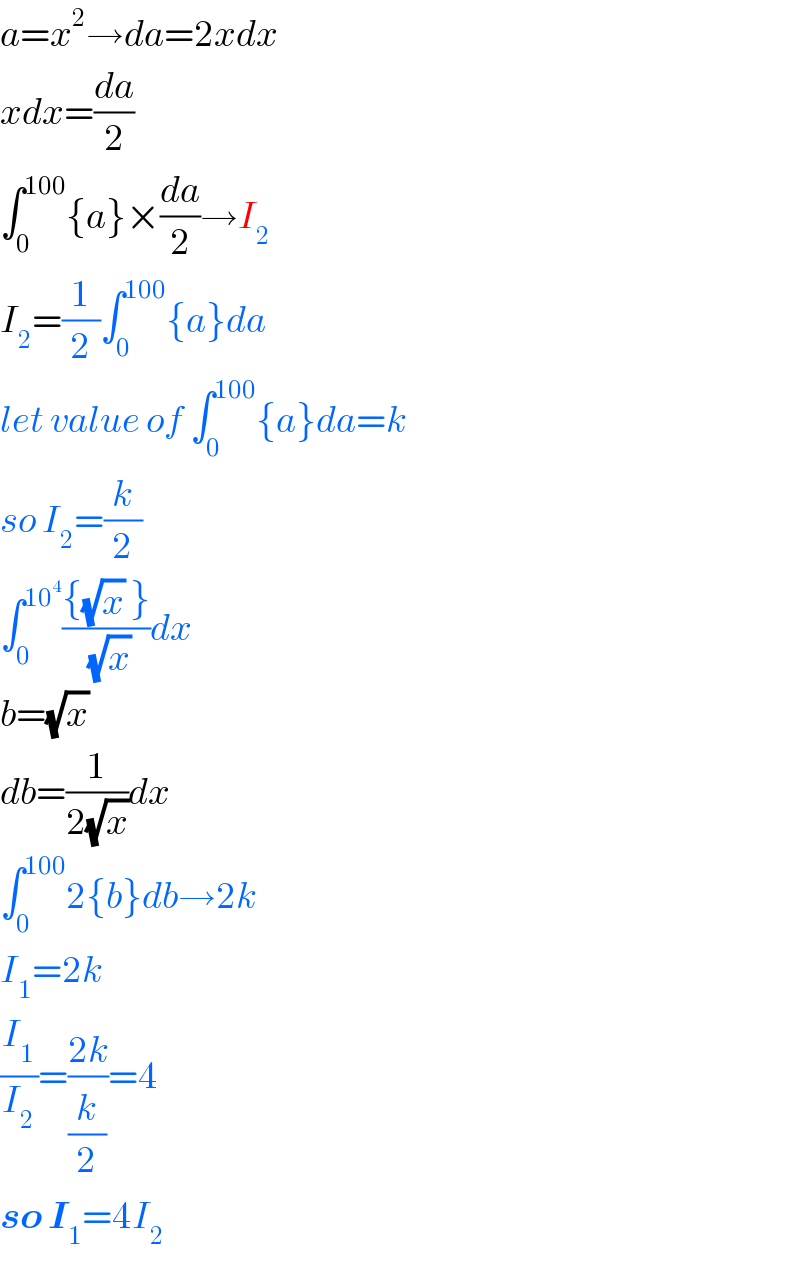
$${a}={x}^{\mathrm{2}} \rightarrow{da}=\mathrm{2}{xdx} \\ $$$${xdx}=\frac{{da}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{100}} \left\{{a}\right\}×\frac{{da}}{\mathrm{2}}\rightarrow{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{100}} \left\{{a}\right\}{da} \\ $$$${let}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{100}} \left\{{a}\right\}{da}={k} \\ $$$${so}\:{I}_{\mathrm{2}} =\frac{{k}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{10}^{\mathrm{4}} } \frac{\left\{\sqrt{{x}}\:\right\}}{\:\sqrt{{x}}}{dx} \\ $$$${b}=\sqrt{{x}}\: \\ $$$${db}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{100}} \mathrm{2}\left\{{b}\right\}{db}\rightarrow\mathrm{2}{k} \\ $$$${I}_{\mathrm{1}} =\mathrm{2}{k} \\ $$$$\frac{{I}_{\mathrm{1}} }{{I}_{\mathrm{2}} }=\frac{\mathrm{2}{k}}{\frac{{k}}{\mathrm{2}}}=\mathrm{4} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}_{\mathrm{1}} =\mathrm{4}{I}_{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 26/Apr/19
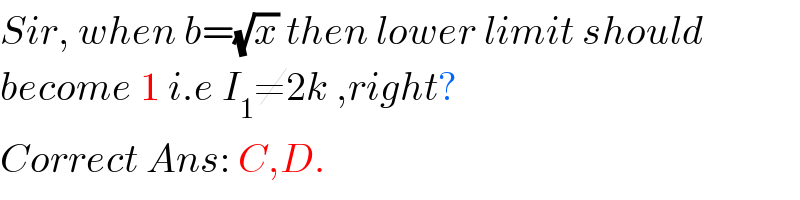
$${Sir},\:{when}\:{b}=\sqrt{{x}}\:{then}\:{lower}\:{limit}\:{should} \\ $$$${become}\:\mathrm{1}\:{i}.{e}\:{I}_{\mathrm{1}} \neq\mathrm{2}{k}\:,{right}? \\ $$$${Correct}\:{Ans}:\:{C},{D}. \\ $$
Commented by tanmay last updated on 26/Apr/19
![lower limit of I_1 =1 but i considered it 0 by mistake when i introduced a and b in place of x^2 and (√x) I_1 and I_2 converted to same pattern... so it is my mistake... (1/2)∫_0 ^(100) {a}da =(1/2)∫_0 ^(100) a−[a] da =(1/2)∫_0 ^(100) ada−(1/2)[∫_0 ^1 [a]da+∫_1 ^2 [a]da+...∫_(99) ^(100) [a]da =(1/2)×∣(a^2 /2)∣_0 ^(100) −(1/2)[∫_0 ^1 0da+∫_1 ^2 1×da+∫_2 ^3 2da+..∫_(99) ^(100) 99da] =(1/2)×((100×100)/2)−(1/2)[0+1+2+..+99] =2500−(1/2)×((99)/2)[2×1+(99−1)×1] =2500−((99)/4)×100 =25(100−99)=25 ∫_1 ^(100) {b}db =∫_1 ^(100) bdb−[∫_1 ^2 1×db+∫_2 ^3 2×db+...+∫_(99) ^(100) 99×db] =((100^2 −1^2 )/2)−[1+2+3+..+99] =((101×99)/2)−((99)/2)[2×1+(99−1)×1] =((101×99)/2)−((99×100)/2) =((99)/2) pls check](https://www.tinkutara.com/question/Q58620.png)
$${lower}\:{limit}\:{of}\:{I}_{\mathrm{1}} =\mathrm{1}\:\:{but}\:{i}\:{considered}\:{it}\:\mathrm{0}\:{by}\:{mistake} \\ $$$${when}\:{i}\:{introduced}\:{a}\:{and}\:{b}\:{in}\:{place}\:{of}\:{x}^{\mathrm{2}} \:{and}\:\sqrt{{x}}\: \\ $$$$\:{I}_{\mathrm{1}} \:{and}\:{I}_{\mathrm{2}} \:{converted}\:{to}\:{same}\:{pattern}… \\ $$$${so}\:{it}\:{is}\:{my}\:{mistake}… \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{100}} \left\{{a}\right\}{da} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{100}} {a}−\left[{a}\right]\:\:{da} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{100}} {ada}−\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\mathrm{1}} \left[{a}\right]{da}+\int_{\mathrm{1}} ^{\mathrm{2}} \left[{a}\right]{da}+…\int_{\mathrm{99}} ^{\mathrm{100}} \left[{a}\right]{da}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mid\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{\mathrm{100}} −\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{0}{da}+\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{1}×{da}+\int_{\mathrm{2}} ^{\mathrm{3}} \mathrm{2}{da}+..\int_{\mathrm{99}} ^{\mathrm{100}} \mathrm{99}{da}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{100}×\mathrm{100}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{0}+\mathrm{1}+\mathrm{2}+..+\mathrm{99}\right] \\ $$$$=\mathrm{2500}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{99}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left(\mathrm{99}−\mathrm{1}\right)×\mathrm{1}\right] \\ $$$$=\mathrm{2500}−\frac{\mathrm{99}}{\mathrm{4}}×\mathrm{100} \\ $$$$=\mathrm{25}\left(\mathrm{100}−\mathrm{99}\right)=\mathrm{25} \\ $$$$ \\ $$$$\int_{\mathrm{1}} ^{\mathrm{100}} \left\{{b}\right\}{db} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{100}} {bdb}−\left[\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{1}×{db}+\int_{\mathrm{2}} ^{\mathrm{3}} \mathrm{2}×{db}+…+\int_{\mathrm{99}} ^{\mathrm{100}} \mathrm{99}×{db}\right] \\ $$$$=\frac{\mathrm{100}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}−\left[\mathrm{1}+\mathrm{2}+\mathrm{3}+..+\mathrm{99}\right] \\ $$$$=\frac{\mathrm{101}×\mathrm{99}}{\mathrm{2}}−\frac{\mathrm{99}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left(\mathrm{99}−\mathrm{1}\right)×\mathrm{1}\right] \\ $$$$=\frac{\mathrm{101}×\mathrm{99}}{\mathrm{2}}−\frac{\mathrm{99}×\mathrm{100}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{99}}{\mathrm{2}} \\ $$$${pls}\:{check} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by rahul 19 last updated on 26/Apr/19
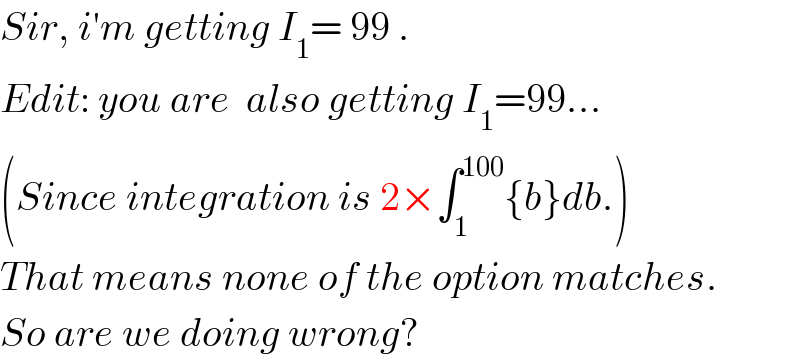
$${Sir},\:{i}'{m}\:{getting}\:{I}_{\mathrm{1}} =\:\mathrm{99}\:. \\ $$$${Edit}:\:{you}\:{are}\:\:{also}\:{getting}\:{I}_{\mathrm{1}} =\mathrm{99}… \\ $$$$\left({Since}\:{integration}\:{is}\:\mathrm{2}×\int_{\mathrm{1}} ^{\mathrm{100}} \left\{{b}\right\}{db}.\right) \\ $$$${That}\:{means}\:{none}\:{of}\:{the}\:{option}\:{matches}. \\ $$$${So}\:{are}\:{we}\:{doing}\:{wrong}?\: \\ $$
Commented by tanmay last updated on 26/Apr/19

$${i}\:{think}\:{no}\:…{we}\:{are}\:{correct}…{option}\:{may}\:{be}\:{wrong} \\ $$$${let}\:{us}\:{use}\:{app}\:{to}\:{find}\:{the}\:{exact}\:{solution} \\ $$
Commented by rahul 19 last updated on 26/Apr/19

$${thank}\:{U}\:{sir}. \\ $$
