Question Number 58696 by ajfour last updated on 27/Apr/19
Commented by ajfour last updated on 27/Apr/19
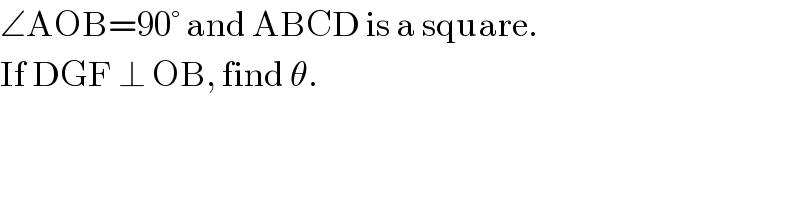
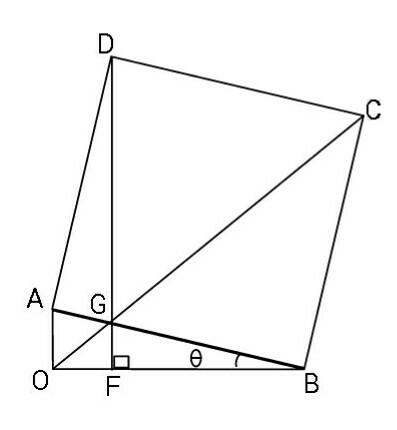
$$\angle\mathrm{AOB}=\mathrm{90}°\:\mathrm{and}\:\mathrm{ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square}. \\ $$$$\mathrm{If}\:\mathrm{DGF}\:\bot\:\mathrm{OB},\:\mathrm{find}\:\theta. \\ $$
Commented by ajfour last updated on 28/Apr/19

$$? \\ $$
Commented by mr W last updated on 28/Apr/19
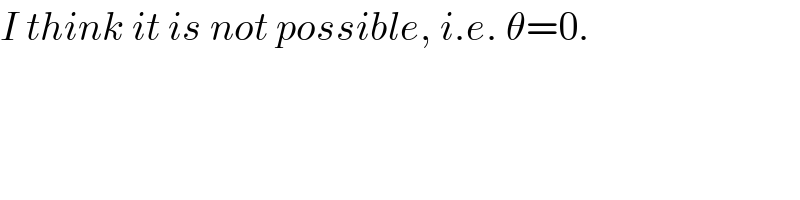
$${I}\:{think}\:{it}\:{is}\:{not}\:{possible},\:{i}.{e}.\:\theta=\mathrm{0}. \\ $$
Answered by mr W last updated on 29/Apr/19

$${GB}={a}−{AG}={a}−{a}\:\mathrm{tan}\:\theta={a}\left(\mathrm{1}−\mathrm{tan}\:\theta\right) \\ $$$$\mathrm{tan}\:\angle{BGC}=\frac{{a}}{{a}\left(\mathrm{1}−\mathrm{tan}\:\theta\right)}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\theta} \\ $$$$\mathrm{tan}\:\angle{GOF}=\frac{{GB}\:\mathrm{sin}\:\theta}{{a}\:\mathrm{sin}\:\theta}=\mathrm{1}−\mathrm{tan}\:\theta \\ $$$$\angle{AGO}=\angle{GOF}+\theta \\ $$$$\mathrm{tan}\:\angle{AGO}=\mathrm{tan}\:\left(\angle{GOF}+\theta\right)=\frac{\mathrm{tan}\:\angle{GOF}+\mathrm{tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:\angle{GOF}\:\mathrm{tan}\:\theta} \\ $$$$=\frac{\mathrm{1}−\mathrm{tan}\:\theta+\mathrm{tan}\:\theta}{\mathrm{1}−\left(\mathrm{1}−\mathrm{tan}\:\theta\right)\:\mathrm{tan}\:\theta}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\theta+\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$${i}.{e}.\:\mathrm{tan}\:\angle{BGC}\neq\mathrm{tan}\:\angle{AGO} \\ $$$$\Rightarrow\angle{BGC}\neq\angle{AGO} \\ $$$$\Rightarrow{AB},\:{CO}\:{and}\:{DF}\:{don}'{t}\:{intersect}\:{on} \\ $$$${the}\:{same}\:{point}\:{G}. \\ $$
Commented by ajfour last updated on 01/May/19

$$\mathrm{its}\:\mathrm{alright}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{was}\:\mathrm{playing}\:\mathrm{blind}.. \\ $$$$\mathrm{sorry}! \\ $$
Commented by mr W last updated on 01/May/19

$${no}\:{reason}\:{to}\:{be}\:{sorry}\:{sir}! \\ $$$${you}\:{have}\:{created}\:{super}\:{questions}. \\ $$
