Question-58754

Question Number 58754 by azizullah last updated on 29/Apr/19

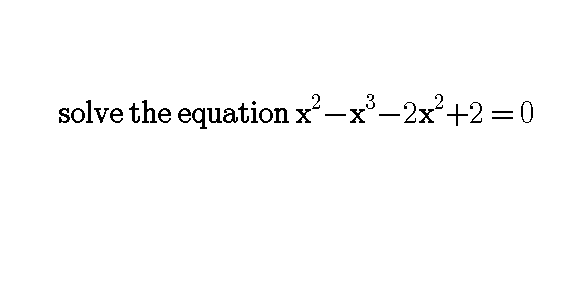
Answered by Rasheed.Sindhi last updated on 29/Apr/19

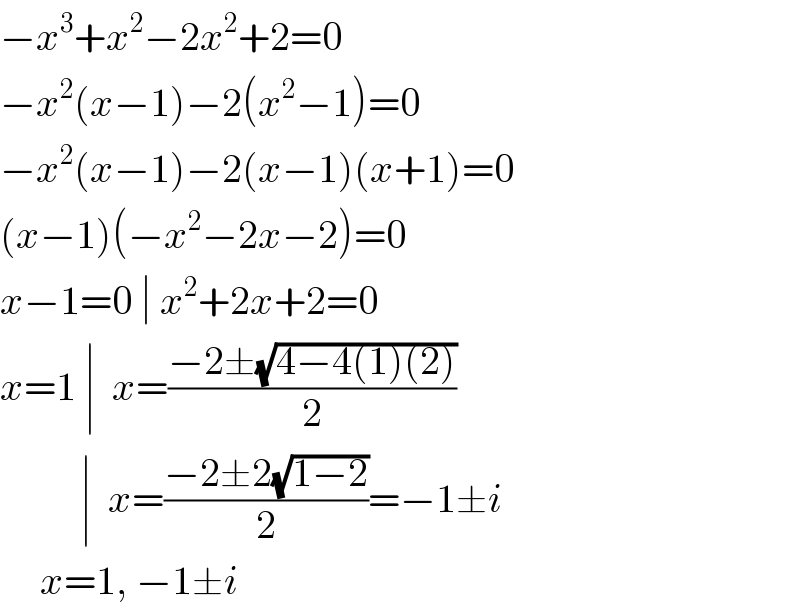
−x^3 +x^2 −2x^2 +2=0 −x^2 (x−1)−2(x^2 −1)=0 −x^2 (x−1)−2(x−1)(x+1)=0 (x−1)(−x^2 −2x−2)=0 x−1=0 ∣ x^2 +2x+2=0 x=1 ∣ x=((−2±(√(4−4(1)(2))))/2) ∣ x=((−2±2(√(1−2)))/2)=−1±i x=1, −1±i

$$−{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}=\mathrm{0} \\ $$$$−{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)−\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$−{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)−\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(−{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$${x}−\mathrm{1}=\mathrm{0}\:\mid\:{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}=\mathrm{1}\:\mid\:\:{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{2}\right)}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mid\:\:{x}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2}}}{\mathrm{2}}=−\mathrm{1}\pm{i} \\ $$$$\:\:\:\:\:{x}=\mathrm{1},\:−\mathrm{1}\pm{i} \\ $$

Commented by azizullah last updated on 30/Apr/19

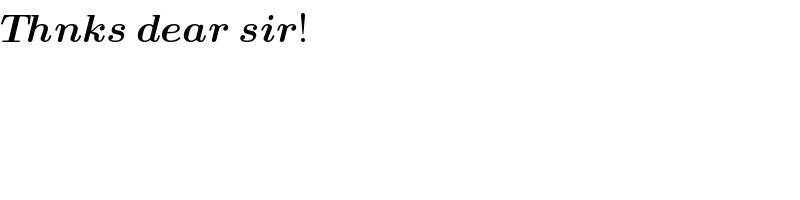
$$\boldsymbol{{Thnks}}\:\boldsymbol{{dear}}\:\boldsymbol{{sir}}! \\ $$

Answered by tanmay last updated on 29/Apr/19

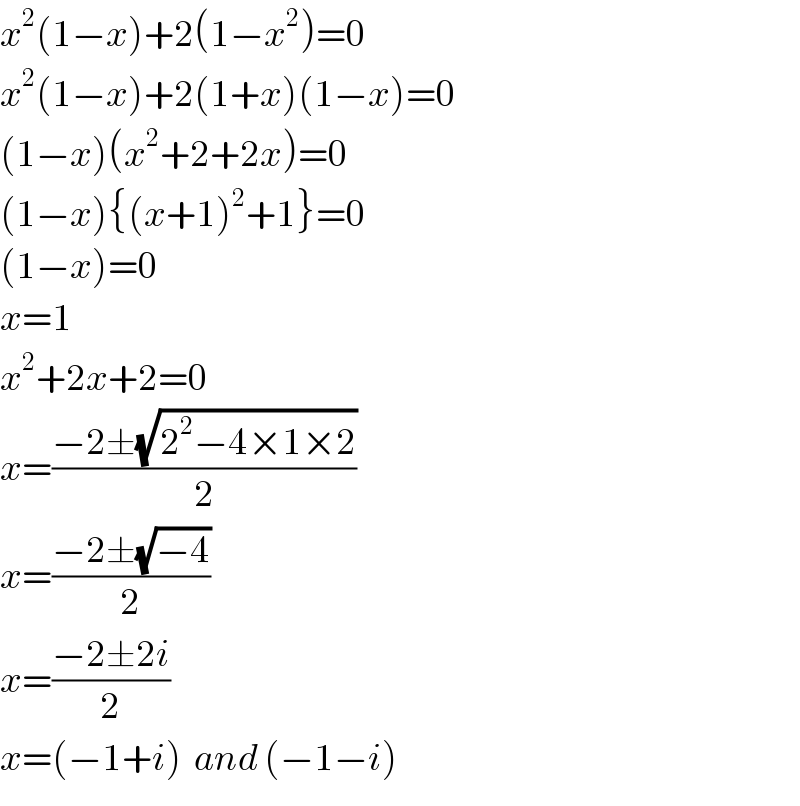
x^2 (1−x)+2(1−x^2 )=0 x^2 (1−x)+2(1+x)(1−x)=0 (1−x)(x^2 +2+2x)=0 (1−x){(x+1)^2 +1}=0 (1−x)=0 x=1 x^2 +2x+2=0 x=((−2±(√(2^2 −4×1×2)))/2) x=((−2±(√(−4)))/2) x=((−2±2i)/2) x=(−1+i) and (−1−i)

$${x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\mathrm{2}\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}\right)\left({x}^{\mathrm{2}} +\mathrm{2}+\mathrm{2}{x}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}\right)\left\{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}=\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{2}^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\mathrm{2}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{2}\pm\sqrt{−\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{2}\pm\mathrm{2}{i}}{\mathrm{2}} \\ $$$${x}=\left(−\mathrm{1}+{i}\right)\:\:{and}\:\left(−\mathrm{1}−{i}\right) \\ $$

Commented by azizullah last updated on 30/Apr/19

$$\boldsymbol{\mathrm{Alot}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{sir}}! \\ $$

Commented by tanmay last updated on 30/Apr/19

$${most}\:{wlcome}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply