Menu Close

Question-58756

Tinku Tara 0 Comments
Pin




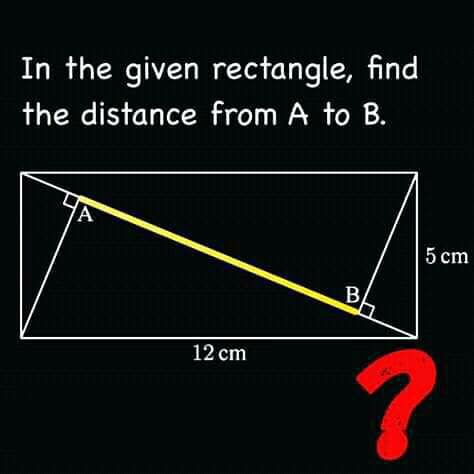
Question Number 58756 by Tawa1 last updated on 29/Apr/19
Answered by Kunal12588 last updated on 29/Apr/19
Commented by Kunal12588 last updated on 29/Apr/19
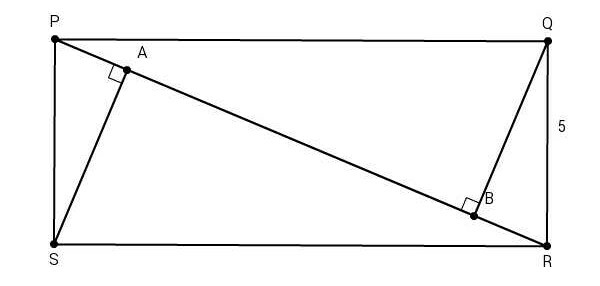
PR=(√(5^2 +12^2 ))=13 cm ∠RBQ=∠RQP [each 90°] ∠QRB=∠PRQ [common] ∴ △BQR ∼△QPR ⇒((BR)/(QR))=((QR)/(PR)) ⇒((BR)/5)=(5/(13)) ⇒BR=((25)/(13)) cm AB=PR−2BR ⇒AB=13−((50)/(13))=((119)/(13)) cm=9.1538... cm
$${PR}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13}\:{cm} \\ $$$$ \\ $$$$\angle{RBQ}=\angle{RQP}\:\:\:\:\:\left[{each}\:\mathrm{90}°\right] \\ $$$$\angle{QRB}=\angle{PRQ}\:\:\:\:\:\left[{common}\right] \\ $$$$\therefore\:\bigtriangleup{BQR}\:\sim\bigtriangleup{QPR}\: \\ $$$$\Rightarrow\frac{{BR}}{{QR}}=\frac{{QR}}{{PR}} \\ $$$$\Rightarrow\frac{{BR}}{\mathrm{5}}=\frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\Rightarrow{BR}=\frac{\mathrm{25}}{\mathrm{13}}\:{cm} \\ $$$${AB}={PR}−\mathrm{2}{BR} \\ $$$$\Rightarrow{AB}=\mathrm{13}−\frac{\mathrm{50}}{\mathrm{13}}=\frac{\mathrm{119}}{\mathrm{13}}\:{cm}=\mathrm{9}.\mathrm{1538}…\:{cm} \\ $$
Commented by Tawa1 last updated on 29/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 30/Apr/19
we have PR^→ .SQ^→ = PR^− .AB^− ( orthogonal projection on line (PQ) =PR.AB also we have PR^→ .SQ^→ =PR^→ .( SP^→ +PQ^→ ) =PR^→ .SP^→ + PR^→ .PQ^→ but PR^→ .SP^→ =SP^− .PS^→ =−SP^2 =−5^2 =−25(orth.proj.on (SP) PR^→ .PQ^→ = PQ^− .PQ^− =PQ^2 =12^2 =144 ⇒ PR .AB =144 −25 =119 ⇒AB =((119)/(PR)) and pythagore theorem give PR =(√(12^2 +5^2 ))=(√(144 +25)) =(√(169))=13 ⇒ AB =((119)/(13)) .
$${we}\:{have}\:\:{P}\overset{\rightarrow} {{R}}\:.{S}\overset{\rightarrow} {{Q}}\:=\:{P}\overset{−} {{R}}.{A}\overset{−} {{B}}\:\:\:\:\left(\:{orthogonal}\:{projection}\:{on}\:{line}\:\left({PQ}\right)\right. \\ $$$$={PR}.{AB}\:\:\:\:\:\:\:{also}\:{we}\:{have}\:\:{P}\overset{\rightarrow} {{R}}.{S}\overset{\rightarrow} {{Q}}={P}\overset{\rightarrow} {{R}}.\left(\:{S}\overset{\rightarrow} {{P}}\:+{P}\overset{\rightarrow} {{Q}}\right) \\ $$$$={P}\overset{\rightarrow} {{R}}.{S}\overset{\rightarrow} {{P}}\:+\:{P}\overset{\rightarrow} {{R}}.{P}\overset{\rightarrow} {{Q}}\:\:\:\:\:{but}\:\:{P}\overset{\rightarrow} {{R}}.{S}\overset{\rightarrow} {{P}}={S}\overset{−} {{P}}.{P}\overset{\rightarrow} {{S}}=−{SP}^{\mathrm{2}} \:=−\mathrm{5}^{\mathrm{2}} =−\mathrm{25}\left({orth}.{proj}.{on}\:\left({SP}\right)\right. \\ $$$${P}\overset{\rightarrow} {{R}}.{P}\overset{\rightarrow} {{Q}}\:=\:{P}\overset{−} {{Q}}.{P}\overset{−} {{Q}}\:={PQ}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} \:=\mathrm{144}\:\Rightarrow\:{PR}\:.{AB}\:=\mathrm{144}\:−\mathrm{25}\:=\mathrm{119} \\ $$$$\Rightarrow{AB}\:=\frac{\mathrm{119}}{{PR}}\:\:\:\:\:\:{and}\:{pythagore}\:{theorem}\:{give}\:{PR}\:=\sqrt{\mathrm{12}^{\mathrm{2}} \:+\mathrm{5}^{\mathrm{2}} \:}=\sqrt{\mathrm{144}\:+\mathrm{25}} \\ $$$$=\sqrt{\mathrm{169}}=\mathrm{13}\:\Rightarrow\:{AB}\:=\frac{\mathrm{119}}{\mathrm{13}}\:. \\ $$
Commented by maxmathsup by imad last updated on 30/Apr/19
here i have used scalar product .
$${here}\:{i}\:{have}\:{used}\:\:{scalar}\:{product}\:. \\ $$
Answered by tanmay last updated on 29/Apr/19
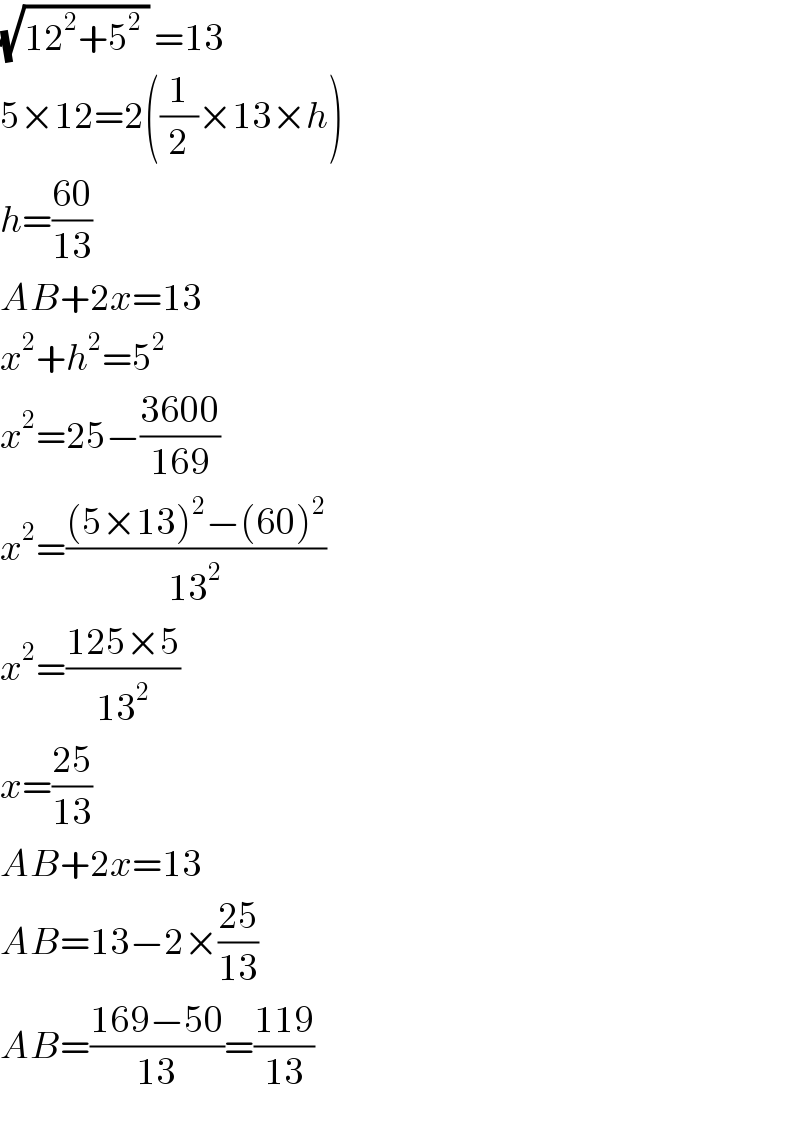
(√(12^2 +5^2 )) =13 5×12=2((1/2)×13×h) h=((60)/(13)) AB+2x=13 x^2 +h^2 =5^2 x^2 =25−((3600)/(169)) x^2 =(((5×13)^2 −(60)^2 )/(13^2 )) x^2 =((125×5)/(13^2 )) x=((25)/(13)) AB+2x=13 AB=13−2×((25)/(13)) AB=((169−50)/(13))=((119)/(13))
$$\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \:}\:=\mathrm{13} \\ $$$$\mathrm{5}×\mathrm{12}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{13}×{h}\right) \\ $$$${h}=\frac{\mathrm{60}}{\mathrm{13}} \\ $$$${AB}+\mathrm{2}{x}=\mathrm{13} \\ $$$${x}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\mathrm{25}−\frac{\mathrm{3600}}{\mathrm{169}} \\ $$$${x}^{\mathrm{2}} =\frac{\left(\mathrm{5}×\mathrm{13}\right)^{\mathrm{2}} −\left(\mathrm{60}\right)^{\mathrm{2}} }{\mathrm{13}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{125}×\mathrm{5}}{\mathrm{13}^{\mathrm{2}} } \\ $$$${x}=\frac{\mathrm{25}}{\mathrm{13}} \\ $$$${AB}+\mathrm{2}{x}=\mathrm{13} \\ $$$${AB}=\mathrm{13}−\mathrm{2}×\frac{\mathrm{25}}{\mathrm{13}} \\ $$$${AB}=\frac{\mathrm{169}−\mathrm{50}}{\mathrm{13}}=\frac{\mathrm{119}}{\mathrm{13}} \\ $$
Commented by Tawa1 last updated on 29/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 29/Apr/19
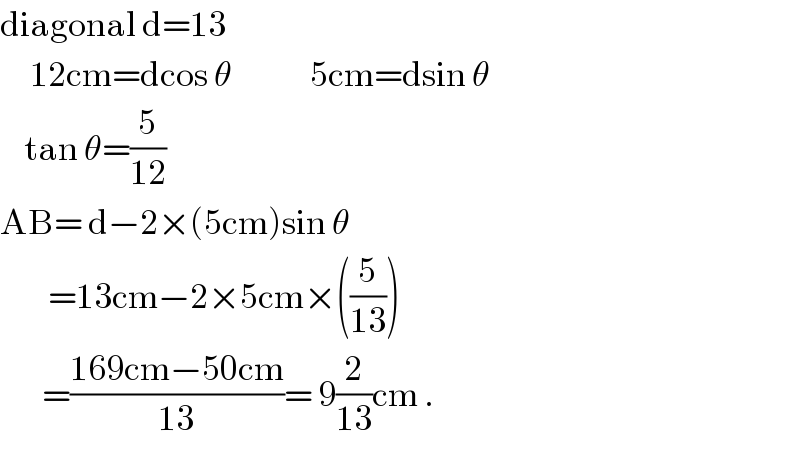
diagonal d=13 12cm=dcos θ 5cm=dsin θ tan θ=(5/(12)) AB= d−2×(5cm)sin θ =13cm−2×5cm×((5/(13))) =((169cm−50cm)/(13))= 9(2/(13))cm .
$$\mathrm{diagonal}\:\mathrm{d}=\mathrm{13} \\ $$$$\:\:\:\:\:\mathrm{12cm}=\mathrm{dcos}\:\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5cm}=\mathrm{dsin}\:\theta \\ $$$$\:\:\:\:\mathrm{tan}\:\theta=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\mathrm{AB}=\:\mathrm{d}−\mathrm{2}×\left(\mathrm{5cm}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{13cm}−\mathrm{2}×\mathrm{5cm}×\left(\frac{\mathrm{5}}{\mathrm{13}}\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{169cm}−\mathrm{50cm}}{\mathrm{13}}=\:\mathrm{9}\frac{\mathrm{2}}{\mathrm{13}}\mathrm{cm}\:. \\ $$
Commented by Tawa1 last updated on 29/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *