Question Number 58789 by ANTARES VY last updated on 30/Apr/19

Commented by ANTARES VY last updated on 30/Apr/19

$$\mathrm{E}=? \\ $$
Commented by tanmay last updated on 30/Apr/19
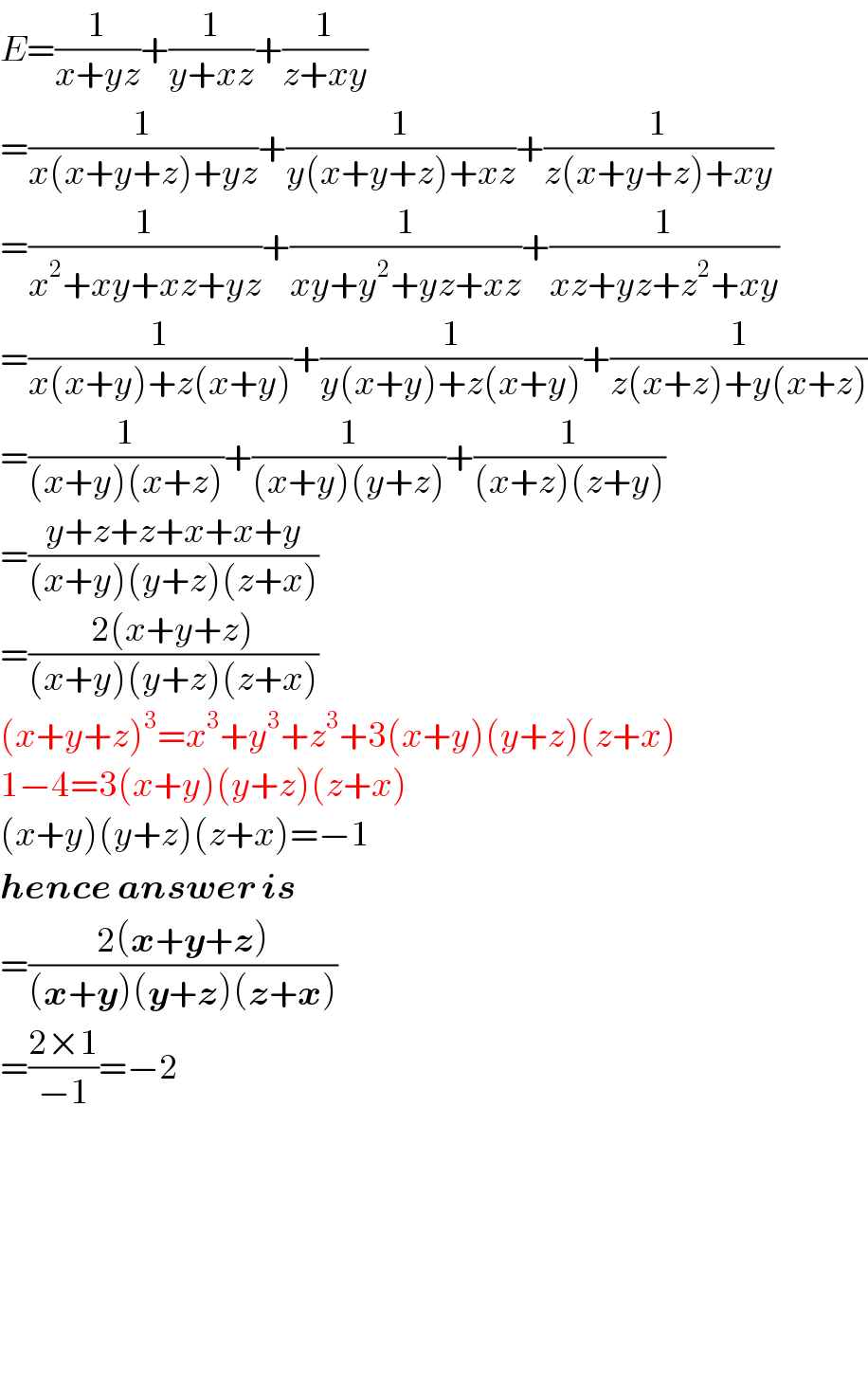
$${E}=\frac{\mathrm{1}}{{x}+{yz}}+\frac{\mathrm{1}}{{y}+{xz}}+\frac{\mathrm{1}}{{z}+{xy}} \\ $$$$=\frac{\mathrm{1}}{{x}\left({x}+{y}+{z}\right)+{yz}}+\frac{\mathrm{1}}{{y}\left({x}+{y}+{z}\right)+{xz}}+\frac{\mathrm{1}}{{z}\left({x}+{y}+{z}\right)+{xy}} \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{xy}+{xz}+{yz}}+\frac{\mathrm{1}}{{xy}+{y}^{\mathrm{2}} +{yz}+{xz}}+\frac{\mathrm{1}}{{xz}+{yz}+{z}^{\mathrm{2}} +{xy}} \\ $$$$=\frac{\mathrm{1}}{{x}\left({x}+{y}\right)+{z}\left({x}+{y}\right)}+\frac{\mathrm{1}}{{y}\left({x}+{y}\right)+{z}\left({x}+{y}\right)}+\frac{\mathrm{1}}{{z}\left({x}+{z}\right)+{y}\left({x}+{z}\right)} \\ $$$$=\frac{\mathrm{1}}{\left({x}+{y}\right)\left({x}+{z}\right)}+\frac{\mathrm{1}}{\left({x}+{y}\right)\left({y}+{z}\right)}+\frac{\mathrm{1}}{\left({x}+{z}\right)\left({z}+{y}\right)} \\ $$$$=\frac{{y}+{z}+{z}+{x}+{x}+{y}}{\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)} \\ $$$$=\frac{\mathrm{2}\left({x}+{y}+{z}\right)}{\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +\mathrm{3}\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right) \\ $$$$\mathrm{1}−\mathrm{4}=\mathrm{3}\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right) \\ $$$$\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)=−\mathrm{1} \\ $$$$\boldsymbol{{hence}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$=\frac{\mathrm{2}\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)}{\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\left(\boldsymbol{{y}}+\boldsymbol{{z}}\right)\left(\boldsymbol{{z}}+\boldsymbol{{x}}\right)} \\ $$$$=\frac{\mathrm{2}×\mathrm{1}}{−\mathrm{1}}=−\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
