Menu Close

Question-58800

Tinku Tara 0 Comments
Pin




Question Number 58800 by naka3546 last updated on 30/Apr/19
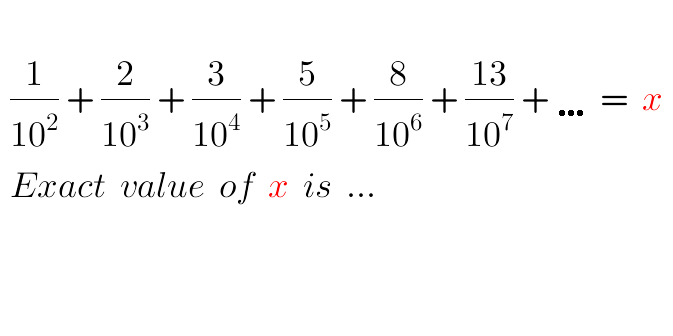
Commented by MJS last updated on 30/Apr/19
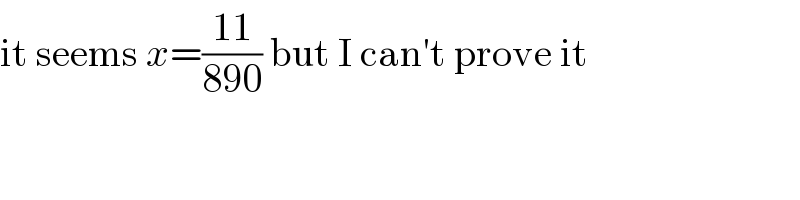
it seems x=((11)/(890)) but I can′t prove it
$$\mathrm{it}\:\mathrm{seems}\:{x}=\frac{\mathrm{11}}{\mathrm{890}}\:\mathrm{but}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{prove}\:\mathrm{it} \\ $$
Commented by tanmay last updated on 30/Apr/19
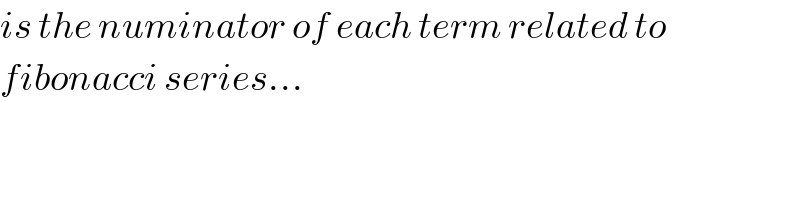
is the numinator of each term related to fibonacci series...
$${is}\:{the}\:{numinator}\:{of}\:{each}\:{term}\:{related}\:{to}\: \\ $$$${fibonacci}\:{series}… \\ $$
Answered by mr W last updated on 30/Apr/19
T_n =(a_n /b_n ) b_n =10^(n+1) a_n −a_(n−1) −a_(n−2) =0 x^2 −x−1=0 x=((1±(√5))/2)=α,β a_n =(α^(n+1) −β^(n+1) )(1/( (√5))) T_n =(1/( (√5)))[((α/(10)))^(n+1) −((β/(10)))^(n+1) ] ← G.P. Σ_(n=1) ^∞ T_n =(α^2 /(100(√5)(1−(α/(10)))))−(β^2 /(100(√5)(1−(β/(10))))) =(((1+(√5))^2 )/(40(√5)(10−((1+(√5))/2))))−(((1−(√5))^2 )/(40(√5)(10−((1−(√5))/2)))) =((6+2(√5))/(20(√5)(19−(√5))))−((6−2(√5))/(20(√5)(19+(√5)))) =(((19+(√5))(6+2(√5))−(19−(√5))(6−2(√5)))/(20(√5)×356)) =(((19×6+44(√5)+10)−(19×6−44(√5)+10))/(20(√5)×356)) =((2×44(√5))/(20(√5)×356)) =((11)/(5×178)) =((11)/(890))
$${T}_{{n}} =\frac{{a}_{{n}} }{{b}_{{n}} } \\ $$$${b}_{{n}} =\mathrm{10}^{{n}+\mathrm{1}} \\ $$$${a}_{{n}} −{a}_{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}=\alpha,\beta \\ $$$${a}_{{n}} =\left(\alpha^{{n}+\mathrm{1}} −\beta^{{n}+\mathrm{1}} \right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\left(\frac{\alpha}{\mathrm{10}}\right)^{{n}+\mathrm{1}} −\left(\frac{\beta}{\mathrm{10}}\right)^{{n}+\mathrm{1}} \right]\:\leftarrow\:{G}.{P}. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{T}_{{n}} =\frac{\alpha^{\mathrm{2}} }{\mathrm{100}\sqrt{\mathrm{5}}\left(\mathrm{1}−\frac{\alpha}{\mathrm{10}}\right)}−\frac{\beta^{\mathrm{2}} }{\mathrm{100}\sqrt{\mathrm{5}}\left(\mathrm{1}−\frac{\beta}{\mathrm{10}}\right)} \\ $$$$=\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{40}\sqrt{\mathrm{5}}\left(\mathrm{10}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)}−\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{40}\sqrt{\mathrm{5}}\left(\mathrm{10}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{20}\sqrt{\mathrm{5}}\left(\mathrm{19}−\sqrt{\mathrm{5}}\right)}−\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{20}\sqrt{\mathrm{5}}\left(\mathrm{19}+\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{\left(\mathrm{19}+\sqrt{\mathrm{5}}\right)\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)−\left(\mathrm{19}−\sqrt{\mathrm{5}}\right)\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{20}\sqrt{\mathrm{5}}×\mathrm{356}} \\ $$$$=\frac{\left(\mathrm{19}×\mathrm{6}+\mathrm{44}\sqrt{\mathrm{5}}+\mathrm{10}\right)−\left(\mathrm{19}×\mathrm{6}−\mathrm{44}\sqrt{\mathrm{5}}+\mathrm{10}\right)}{\mathrm{20}\sqrt{\mathrm{5}}×\mathrm{356}} \\ $$$$=\frac{\mathrm{2}×\mathrm{44}\sqrt{\mathrm{5}}}{\mathrm{20}\sqrt{\mathrm{5}}×\mathrm{356}} \\ $$$$=\frac{\mathrm{11}}{\mathrm{5}×\mathrm{178}} \\ $$$$=\frac{\mathrm{11}}{\mathrm{890}} \\ $$
Commented by MJS last updated on 30/Apr/19
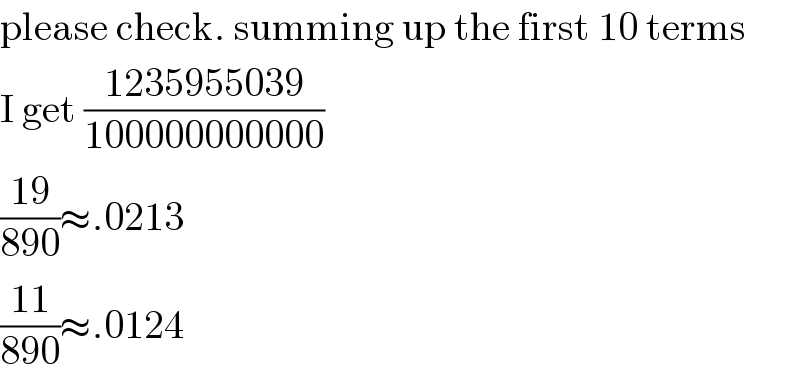
please check. summing up the first 10 terms I get ((1235955039)/(100000000000)) ((19)/(890))≈.0213 ((11)/(890))≈.0124
$$\mathrm{please}\:\mathrm{check}.\:\mathrm{summing}\:\mathrm{up}\:\mathrm{the}\:\mathrm{first}\:\mathrm{10}\:\mathrm{terms} \\ $$$$\mathrm{I}\:\mathrm{get}\:\frac{\mathrm{1235955039}}{\mathrm{100000000000}} \\ $$$$\frac{\mathrm{19}}{\mathrm{890}}\approx.\mathrm{0213} \\ $$$$\frac{\mathrm{11}}{\mathrm{890}}\approx.\mathrm{0124} \\ $$
Commented by mr W last updated on 30/Apr/19
thanks sir! your answer is correct. i found my mistake.
$${thanks}\:{sir}!\:{your}\:{answer}\:{is}\:{correct}.\:{i} \\ $$$${found}\:{my}\:{mistake}. \\ $$
Commented by MJS last updated on 30/Apr/19
you′re welcome thanks for the proof!
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{proof}! \\ $$
Answered by Smail last updated on 30/Apr/19
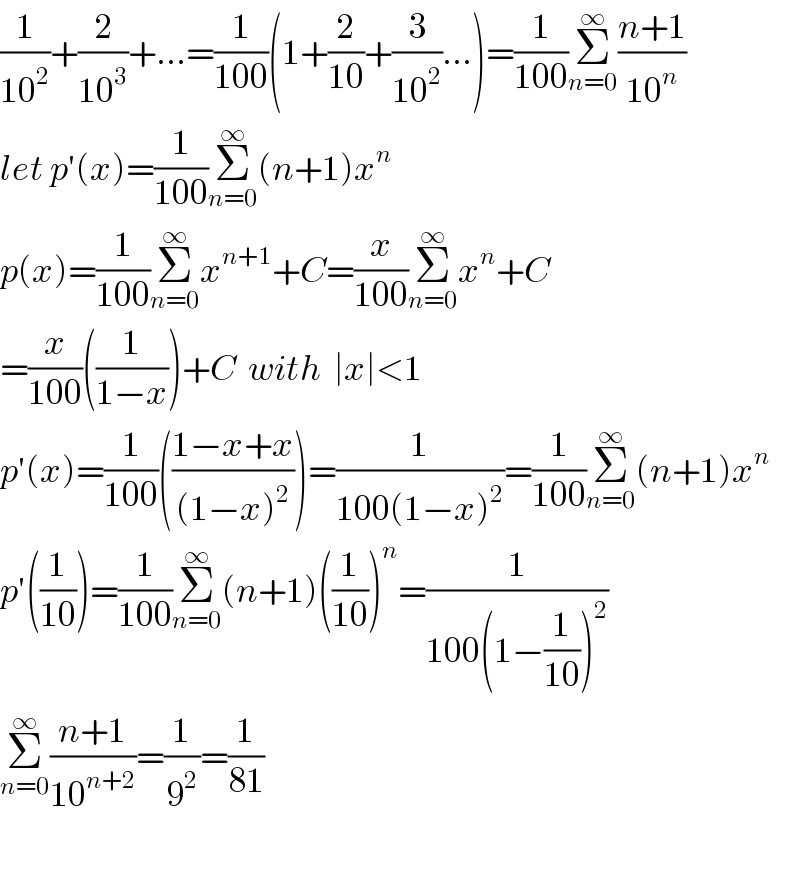
(1/(10^2 ))+(2/(10^3 ))+...=(1/(100))(1+(2/(10))+(3/(10^2 ))...)=(1/(100))Σ_(n=0) ^∞ ((n+1)/(10^n )) let p′(x)=(1/(100))Σ_(n=0) ^∞ (n+1)x^n p(x)=(1/(100))Σ_(n=0) ^∞ x^(n+1) +C=(x/(100))Σ_(n=0) ^∞ x^n +C =(x/(100))((1/(1−x)))+C with ∣x∣<1 p′(x)=(1/(100))(((1−x+x)/((1−x)^2 )))=(1/(100(1−x)^2 ))=(1/(100))Σ_(n=0) ^∞ (n+1)x^n p′((1/(10)))=(1/(100))Σ_(n=0) ^∞ (n+1)((1/(10)))^n =(1/(100(1−(1/(10)))^2 )) Σ_(n=0) ^∞ ((n+1)/(10^(n+2) ))=(1/9^2 )=(1/(81))
$$\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{10}^{\mathrm{3}} }+…=\frac{\mathrm{1}}{\mathrm{100}}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{10}^{\mathrm{2}} }…\right)=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{1}}{\mathrm{10}^{{n}} } \\ $$$${let}\:{p}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \\ $$$${p}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}+\mathrm{1}} +{C}=\frac{{x}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} +{C} \\ $$$$=\frac{{x}}{\mathrm{100}}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)+{C}\:\:{with}\:\:\mid{x}\mid<\mathrm{1} \\ $$$${p}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{100}}\left(\frac{\mathrm{1}−{x}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{100}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \\ $$$${p}'\left(\frac{\mathrm{1}}{\mathrm{10}}\right)=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{{n}} =\frac{\mathrm{1}}{\mathrm{100}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{1}}{\mathrm{10}^{{n}+\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{81}} \\ $$$$ \\ $$
Commented by mr W last updated on 30/Apr/19
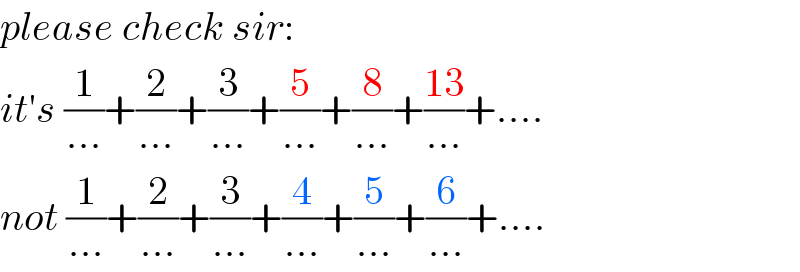
please check sir: it′s (1/(...))+(2/(...))+(3/(...))+(5/(...))+(8/(...))+((13)/(...))+.... not (1/(...))+(2/(...))+(3/(...))+(4/(...))+(5/(...))+(6/(...))+....
$${please}\:{check}\:{sir}:\: \\ $$$${it}'{s}\:\frac{\mathrm{1}}{…}+\frac{\mathrm{2}}{…}+\frac{\mathrm{3}}{…}+\frac{\mathrm{5}}{…}+\frac{\mathrm{8}}{…}+\frac{\mathrm{13}}{…}+…. \\ $$$${not}\:\frac{\mathrm{1}}{…}+\frac{\mathrm{2}}{…}+\frac{\mathrm{3}}{…}+\frac{\mathrm{4}}{…}+\frac{\mathrm{5}}{…}+\frac{\mathrm{6}}{…}+…. \\ $$
Commented by Smail last updated on 30/Apr/19
Thank you for noticing. I did notice the other terms.
$${Thank}\:{you}\:{for}\:{noticing}.\:{I}\:{did}\:{notice}\:{the}\:{other}\:{terms}. \\ $$$$ \\ $$
Commented by mr W last updated on 30/Apr/19
please let your answer stay. though it′s not for this question, but the method is great.
$${please}\:{let}\:{your}\:{answer}\:{stay}.\:{though} \\ $$$${it}'{s}\:{not}\:{for}\:{this}\:{question},\:{but}\:{the} \\ $$$${method}\:{is}\:{great}. \\ $$
Commented by maxmathsup by imad last updated on 30/Apr/19
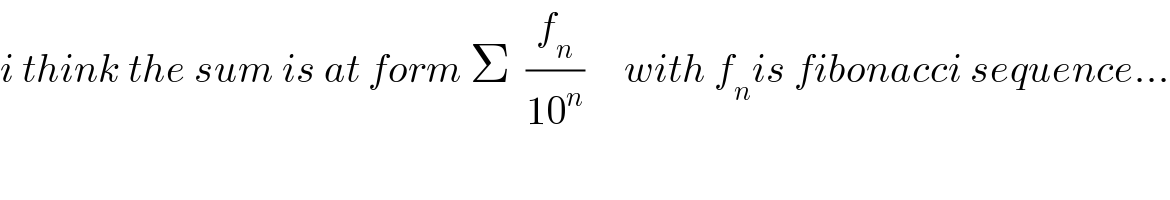
i think the sum is at form Σ (f_n /(10^n )) with f_n is fibonacci sequence...
$${i}\:{think}\:{the}\:{sum}\:{is}\:{at}\:{form}\:\Sigma\:\:\frac{{f}_{{n}} }{\mathrm{10}^{{n}} }\:\:\:\:\:{with}\:{f}_{{n}} {is}\:{fibonacci}\:{sequence}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *