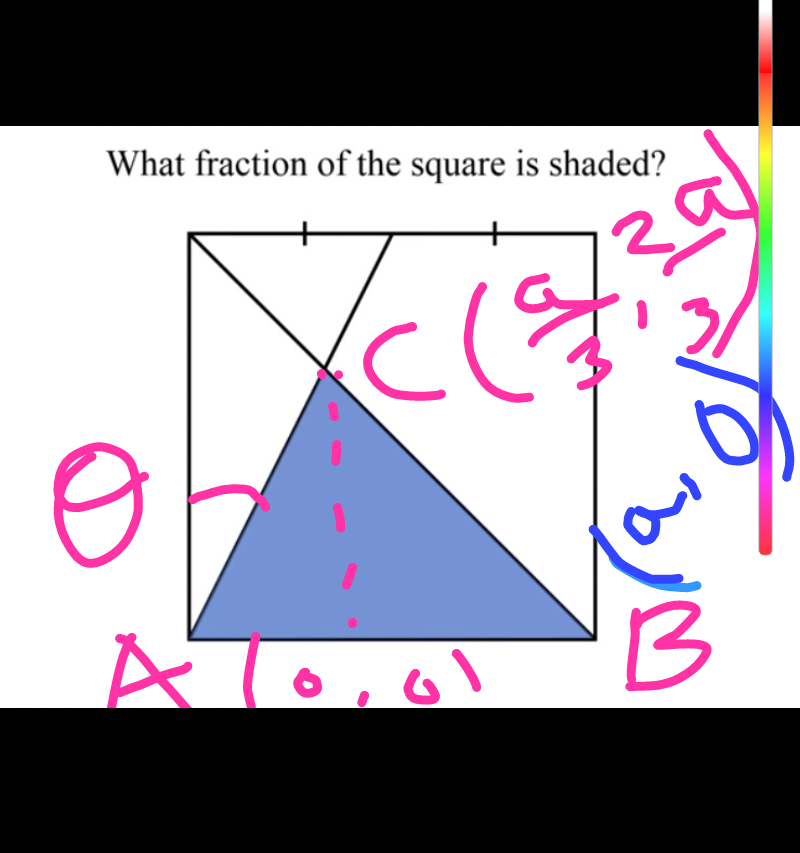
Question Number 58876 by mr W last updated on 01/May/19
Commented by math1967 last updated on 01/May/19

$${Is}\:{it}\:\frac{\mathrm{1}}{\mathrm{3}}\:{part}\:{sir}? \\ $$
Commented by mr W last updated on 01/May/19

$${correct}\:{sir}! \\ $$
Commented by math1967 last updated on 01/May/19
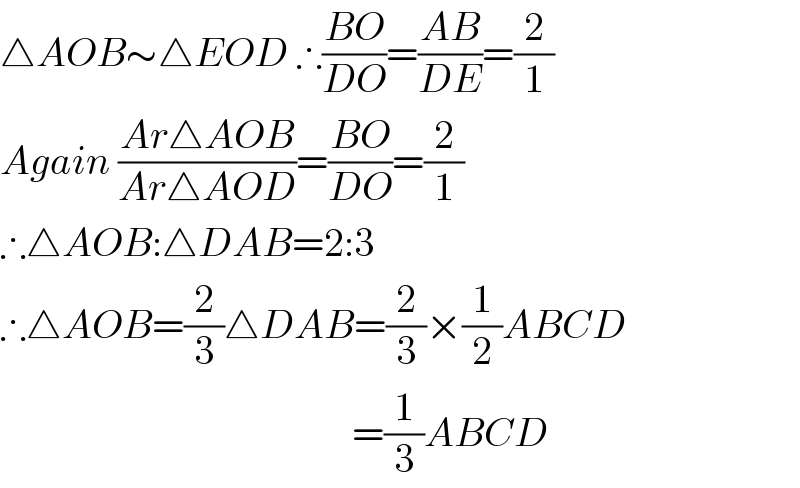
$$\bigtriangleup{AOB}\sim\bigtriangleup{EOD}\:\therefore\frac{{BO}}{{DO}}=\frac{{AB}}{{DE}}=\frac{\mathrm{2}}{\mathrm{1}} \\ $$$${Again}\:\frac{{Ar}\bigtriangleup{AOB}}{{Ar}\bigtriangleup{AOD}}=\frac{{BO}}{{DO}}=\frac{\mathrm{2}}{\mathrm{1}} \\ $$$$\therefore\bigtriangleup{AOB}:\bigtriangleup{DAB}=\mathrm{2}:\mathrm{3} \\ $$$$\therefore\bigtriangleup{AOB}=\frac{\mathrm{2}}{\mathrm{3}}\bigtriangleup{DAB}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}{ABCD}\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}{ABCD} \\ $$
Commented by math1967 last updated on 01/May/19
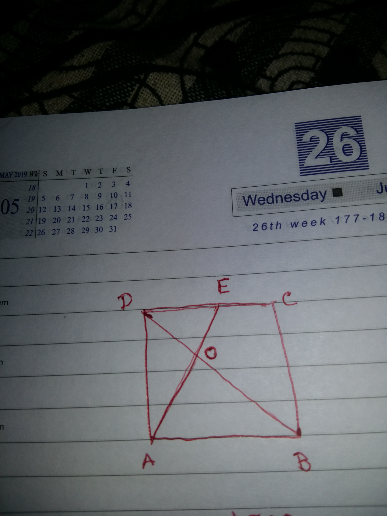
Answered by tanmay last updated on 01/May/19

$${tan}\theta=\frac{\frac{{a}}{\mathrm{2}}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${the}\:{eq}\:{of}\:{st}\:{lines}\:{which}\:{enclose}\:{the}\:{shaded}\:{area} \\ $$$$\left(\mathrm{1}\right)\:{x}\:{axis}\:\:\:\left(\mathrm{2}\right)\:\frac{{x}}{{a}}+\frac{{y}}{{a}}=\mathrm{1}\left(\mathrm{3}\right)\:\:{y}={tan}\left(\mathrm{90}−\theta\right){x} \\ $$$${y}={cot}\theta{x}\rightarrow{y}=\mathrm{2}{x} \\ $$$${now}\:{solve}\:{y}=\mathrm{2}{x}\:{and}\:{x}+{y}={a} \\ $$$$\mathrm{3}{x}={a}\:\:{x}=\frac{{a}}{\mathrm{3}}\:{and}\:{y}=\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$${the}\:{shaded}\:{triangle}\:\:{say}\:{ABC} \\ $$$${point}\:{A}\left(\mathrm{0},\mathrm{0}\right)\:\:{B}\left({a},\mathrm{0}\right)\:\:{C}\left(\frac{{a}}{\mathrm{3}},\frac{\mathrm{2}{a}}{\mathrm{3}}\right) \\ $$$${area}\:{of}\:\bigtriangleup{ABC}=\frac{\mathrm{1}}{\mathrm{2}}×{a}×\frac{\mathrm{2}{a}}{\mathrm{3}}=\frac{{a}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${area}\:{of}\:{shaded}\:{triangle}=\frac{\mathrm{1}}{\mathrm{3}}\left({area}\:{of}\:{square}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay last updated on 01/May/19