Question Number 58877 by Pk1167156@gmail.com last updated on 01/May/19
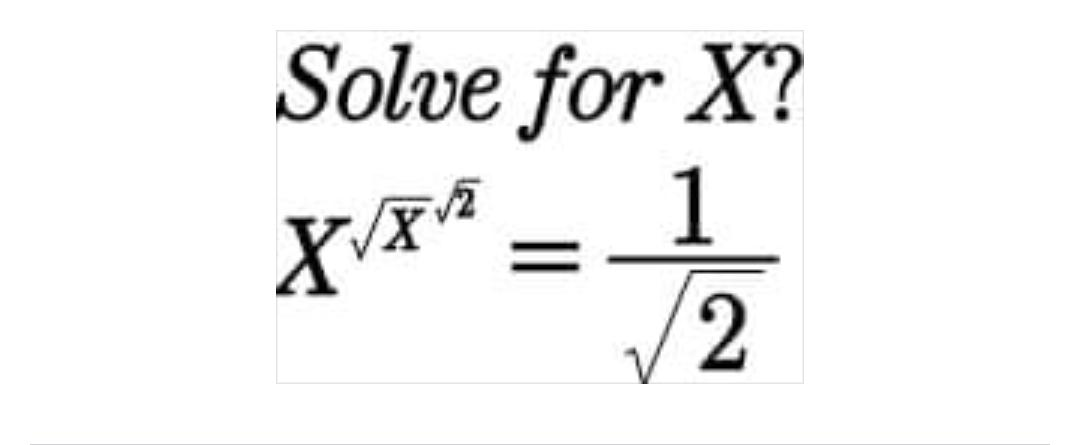
Commented by Pk1167156@gmail.com last updated on 01/May/19
solve for x!!
Commented by MJS last updated on 01/May/19
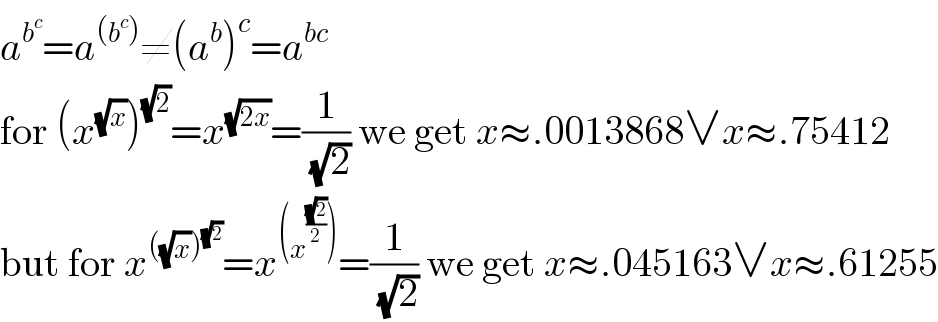
$${a}^{{b}^{{c}} } ={a}^{\left({b}^{{c}} \right)} \neq\left({a}^{{b}} \right)^{{c}} ={a}^{{bc}} \\ $$$$\mathrm{for}\:\left({x}^{\sqrt{{x}}} \right)^{\sqrt{\mathrm{2}}} ={x}^{\sqrt{\mathrm{2}{x}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{we}\:\mathrm{get}\:{x}\approx.\mathrm{0013868}\vee{x}\approx.\mathrm{75412} \\ $$$$\mathrm{but}\:\mathrm{for}\:{x}^{\left(\sqrt{{x}}\right)^{\sqrt{\mathrm{2}}} } ={x}^{\left({x}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \right)} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{we}\:\mathrm{get}\:{x}\approx.\mathrm{045163}\vee{x}\approx.\mathrm{61255} \\ $$
Answered by mr W last updated on 01/May/19
![let t=x^(√x) t^(√2) =(1/( (√2))) (√2) ln t=−(1/2)ln 2 ln t=−((ln 2)/(2(√2))) t=e^(−((ln 2)/(2(√2)))) x^(√x) =t (√x) ln x=ln t=−((ln 2)/(2(√2))) let s=(√x) 2s ln s=−((ln 2)/(2(√2))) ln s^s =−((ln 2)/(4(√2))) s^s =e^(−((ln 2)/(4(√2)))) =a s=a^(1/s) =e^((ln a)/s) (1/s)e^((ln a)/s) =1 ((ln a)/s)e^((ln a)/s) =ln a ((ln a)/s)=W(ln a)=Lambert function s=((ln a)/(W(ln a)))=((−((ln 2)/(4(√2))))/(W(−((ln 2)/(4(√2)))))) x=s^2 ⇒x=[−(((ln 2)/(4(√2)))/(W(−((ln 2)/(4(√2))))))]^2 ≈ { (((((−((ln 2)/(4(√2))))/(−0.14110091)))^2 =0.754121)),(((((−((ln 2)/(4(√2))))/(−3.29038565))))^2 =0.001387)) :}](https://www.tinkutara.com/question/Q58886.png)
$${let}\:{t}={x}^{\sqrt{{x}}} \\ $$$${t}^{\sqrt{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{ln}\:{t}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{ln}\:{t}=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${t}={e}^{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$$${x}^{\sqrt{{x}}} ={t} \\ $$$$\sqrt{{x}}\:\mathrm{ln}\:{x}=\mathrm{ln}\:{t}=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${let}\:{s}=\sqrt{{x}} \\ $$$$\mathrm{2}{s}\:\mathrm{ln}\:{s}=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{ln}\:{s}^{{s}} =−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${s}^{{s}} ={e}^{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}} ={a} \\ $$$${s}={a}^{\frac{\mathrm{1}}{{s}}} ={e}^{\frac{\mathrm{ln}\:{a}}{{s}}} \\ $$$$\frac{\mathrm{1}}{{s}}{e}^{\frac{\mathrm{ln}\:{a}}{{s}}} =\mathrm{1} \\ $$$$\frac{\mathrm{ln}\:{a}}{{s}}{e}^{\frac{\mathrm{ln}\:{a}}{{s}}} =\mathrm{ln}\:{a} \\ $$$$\frac{\mathrm{ln}\:{a}}{{s}}={W}\left(\mathrm{ln}\:{a}\right)={Lambert}\:{function} \\ $$$${s}=\frac{\mathrm{ln}\:{a}}{{W}\left(\mathrm{ln}\:{a}\right)}=\frac{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}}{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)} \\ $$$${x}={s}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\left[−\frac{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}}{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)}\right]^{\mathrm{2}} \approx\begin{cases}{\left(\frac{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}}{−\mathrm{0}.\mathrm{14110091}}\right)^{\mathrm{2}} =\mathrm{0}.\mathrm{754121}}\\{\left(\frac{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}}}{\left.−\mathrm{3}.\mathrm{29038565}\right)}\right)^{\mathrm{2}} =\mathrm{0}.\mathrm{001387}}\end{cases} \\ $$
Commented by otchereabdullai@gmail.com last updated on 01/May/19

$$\mathrm{Brilliant}\:\mathrm{prof}\:\mathrm{W}\:\:\mathrm{i}\:\mathrm{would}\:\mathrm{like}\:\mathrm{to}\:\mathrm{name} \\ $$$$\mathrm{my}\:\mathrm{incoming}\:\mathrm{Baby}\:\mathrm{after}\:\mathrm{you}\:\mathrm{so}\:\mathrm{please}\:\mathrm{if}\: \\ $$$$\mathrm{interested}\:\mathrm{send}\:\mathrm{me}\:\mathrm{your}\:\mathrm{name}\:\mathrm{through} \\ $$$$\mathrm{my}\:\mathrm{e}−\mathrm{mail}\:\:\mathrm{thus}\:\mathrm{my}\:\mathrm{user}\:\mathrm{name}\:\mathrm{thanks} \\ $$
Commented by mr W last updated on 01/May/19

$${Thank}\:{you}\:{for}\:{your}\:{kindness}\:{sir}! \\ $$$${Sorry},\:{but}\:{I}\:{don}'{t}\:{have}\:{such}\:{a}\:{name} \\ $$$${which}\:{is}\:{nice}\:{enough}\:{for}\:{your}\:{baby}. \\ $$$${Nevertheless}\:{I}\:{send}\:{your}\:{incoming} \\ $$$${baby}\:{all}\:{my}\:{best}\:{wishes}! \\ $$
Commented by Tawa1 last updated on 01/May/19

$$\mathrm{Nice}\:\mathrm{solution}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{always} \\ $$
Commented by Tawa1 last updated on 01/May/19

$$\mathrm{Sir},\:\:\mathrm{see}\:\mathrm{question}\:\:\mathrm{58899} \\ $$
Commented by Pk1167156@gmail.com last updated on 01/May/19
very nice sir!!
God bless you!!
Commented by otchereabdullai@gmail.com last updated on 01/May/19
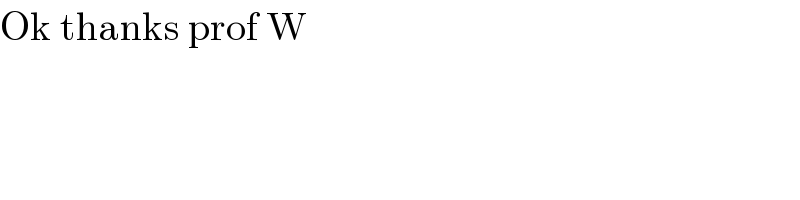
$$\mathrm{Ok}\:\mathrm{thanks}\:\mathrm{prof}\:\mathrm{W} \\ $$
