Question Number 58979 by jahanara@gmail.com last updated on 02/May/19
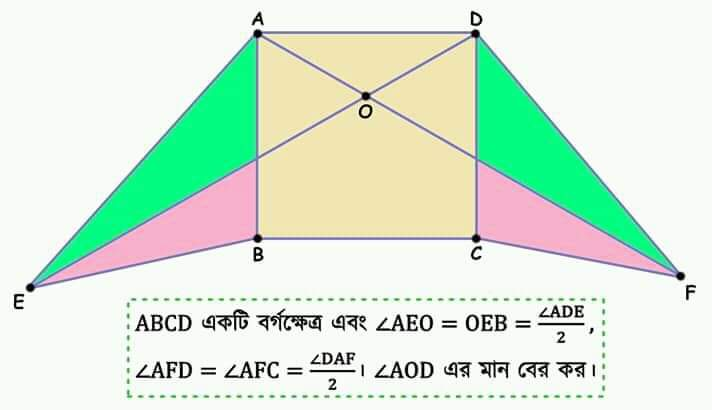
Commented by jahanara@gmail.com last updated on 02/May/19

$${here}\:{abcd}\:{is}\:{a}\:{square}.{find}\:{the}\:{value}\:{of}\:<{aod} \\ $$
Answered by MJS last updated on 03/May/19

$$\angle{ADE}=\alpha \\ $$$$\mathrm{the}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{the}\:\mathrm{green}\:\mathrm{triangle}\:\mathrm{are} \\ $$$$\angle{E}_{{green}} =\frac{\alpha}{\mathrm{2}};\:\angle{A}=\mathrm{90}°−\frac{\mathrm{3}\alpha}{\mathrm{2}}\:\mathrm{and}\:\mathrm{90}°+\alpha \\ $$$$\mathrm{the}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:{AEB}\:\mathrm{are} \\ $$$$\angle{A}=\mathrm{90}°−\frac{\mathrm{3}\alpha}{\mathrm{2}};\:\angle{B}=\mathrm{90}°+\frac{\alpha}{\mathrm{2}};\:\angle{E}=\alpha \\ $$$$\mathrm{putting}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:=\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{using}\:\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\beta}=\frac{{c}}{\mathrm{sin}\:\gamma} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{green}\:\mathrm{triangle}:\:{AE}=\mathrm{2cos}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{triangle}\:{AEB}:\:{AE}=\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow \\ $$$$\mathrm{2cos}\:\frac{\alpha}{\mathrm{2}}\:=\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow\:\mathrm{sin}\:\alpha\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\alpha=\mathrm{30}° \\ $$$$\Rightarrow\:\angle{AOD}=\mathrm{120}° \\ $$
