Question Number 59012 by cesar.marval.larez@gmail.com last updated on 03/May/19
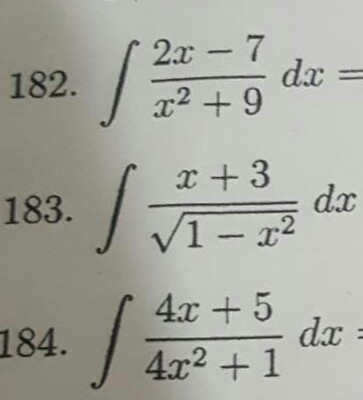
Answered by tanmay last updated on 03/May/19
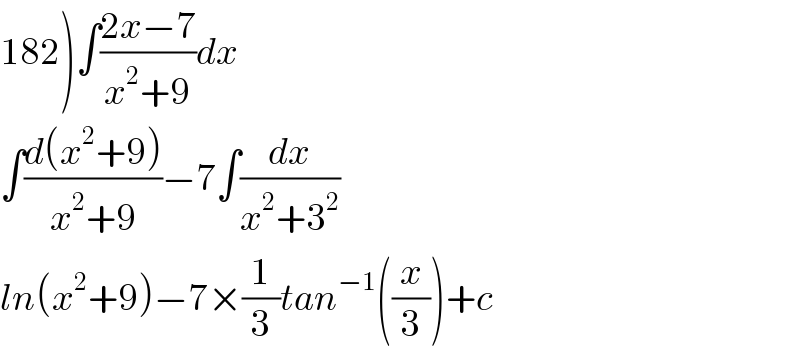
$$\left.\mathrm{182}\right)\int\frac{\mathrm{2}{x}−\mathrm{7}}{{x}^{\mathrm{2}} +\mathrm{9}}{dx} \\ $$$$\int\frac{{d}\left({x}^{\mathrm{2}} +\mathrm{9}\right)}{{x}^{\mathrm{2}} +\mathrm{9}}−\mathrm{7}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} } \\ $$$${ln}\left({x}^{\mathrm{2}} +\mathrm{9}\right)−\mathrm{7}×\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)+{c} \\ $$
Answered by tanmay last updated on 03/May/19
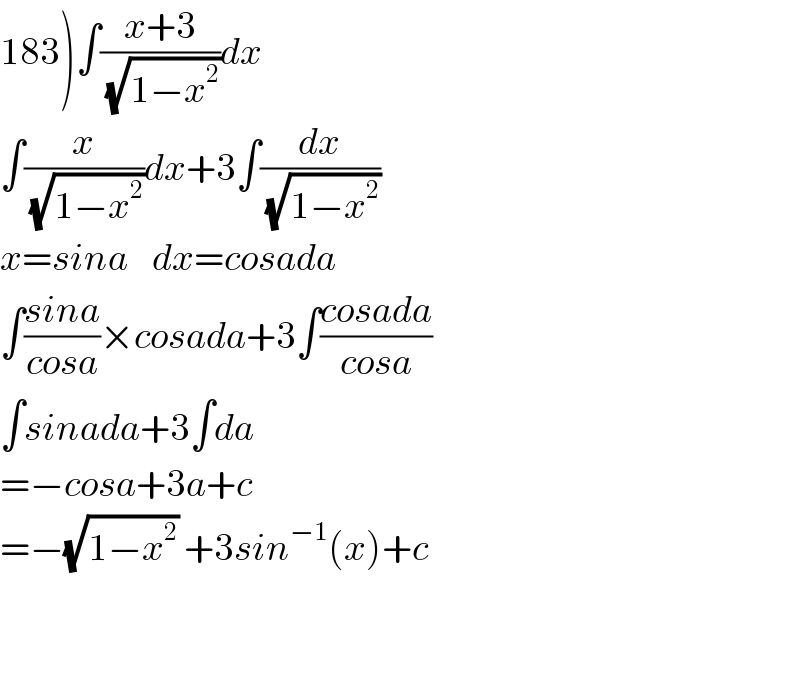
$$\left.\mathrm{183}\right)\int\frac{{x}+\mathrm{3}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+\mathrm{3}\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${x}={sina}\:\:\:\:{dx}={cosada} \\ $$$$\int\frac{{sina}}{{cosa}}×{cosada}+\mathrm{3}\int\frac{{cosada}}{{cosa}} \\ $$$$\int{sinada}+\mathrm{3}\int{da} \\ $$$$=−{cosa}+\mathrm{3}{a}+{c} \\ $$$$=−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\mathrm{3}{sin}^{−\mathrm{1}} \left({x}\right)+{c} \\ $$$$ \\ $$$$ \\ $$
Answered by tanmay last updated on 03/May/19
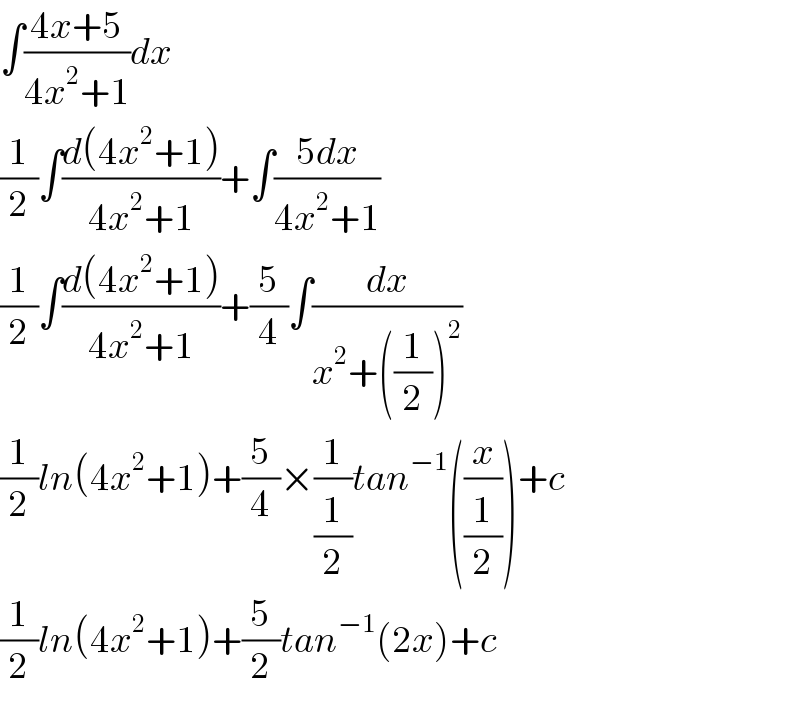
$$\int\frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}+\int\frac{\mathrm{5}{dx}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{5}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\frac{\mathrm{1}}{\mathrm{2}}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)+{c} \\ $$
