Question Number 59892 by rahul 19 last updated on 15/May/19
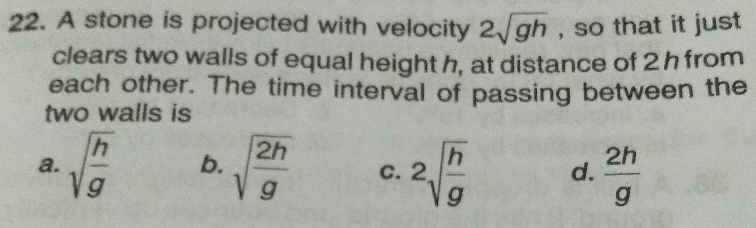
Commented by rahul 19 last updated on 15/May/19

$${Sir}\:,{ans}.\:{is}\:\left({c}\right)! \\ $$
Commented by tanmay last updated on 15/May/19

$${i}\:{found}\:{answer}… \\ $$
Answered by tanmay last updated on 15/May/19

Commented by tanmay last updated on 15/May/19

Commented by rahul 19 last updated on 16/May/19

$${thanks}\:{sir}! \\ $$
Answered by mr W last updated on 15/May/19
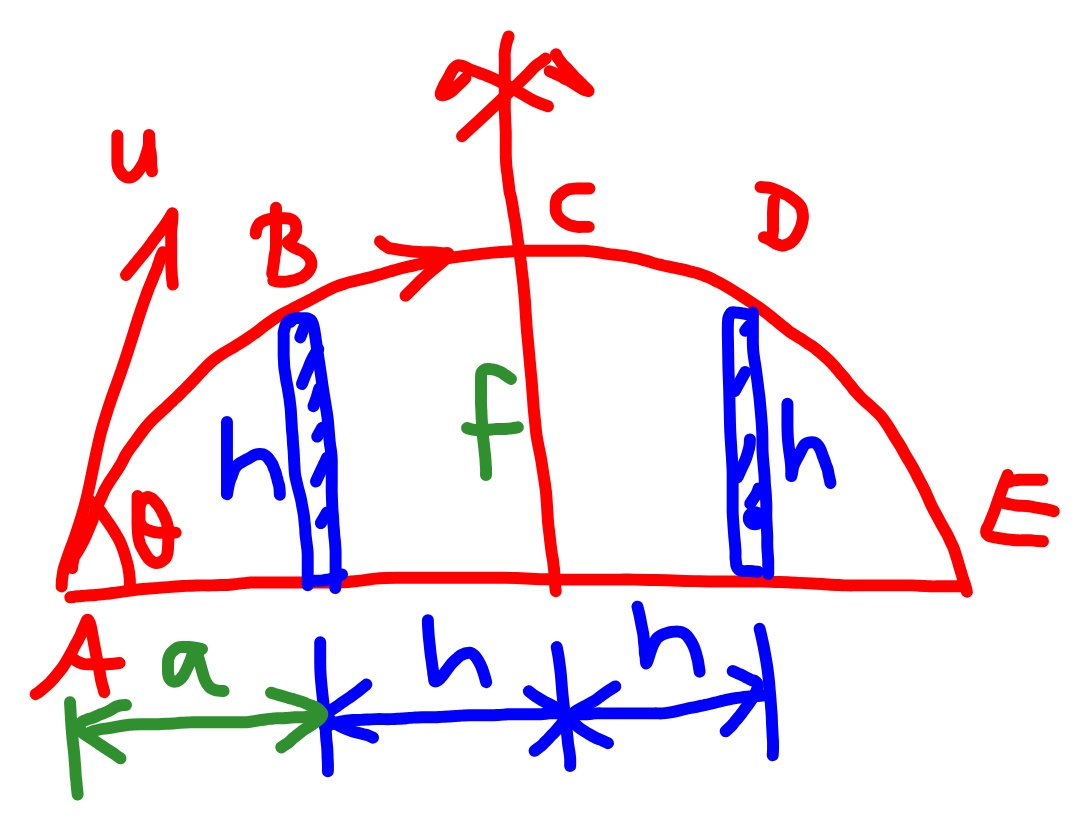
Commented by mr W last updated on 15/May/19
/g)−(h/(u cos θ))) h=(1/(2g))(u^2 sin^2 θ−((g^2 h^2 )/(u^2 cos^2 θ))) h=(1/(2g))(4gh sin^2 θ−((g^2 h^2 )/(4gh cos^2 θ))) 1=2 sin^2 θ−(1/(8 cos^2 θ)) 1=2−2 cos^2 θ−(1/(8 cos^2 θ)) 16 cos^4 θ−8 cos^2 θ+1=0 (4 cos^2 θ−1)^2 =0 ⇒cos^2 θ=(1/4) ⇒cos θ=(1/2) ⇒θ=(π/3)=60° t_2 =((2(√(gh)))/g)×((√3)/2)=(√((3h)/g)) t_1 =((2(√(gh)))/g)×((√3)/2)−(h/(2(√(gh))×(1/2)))=(√((3h)/g))−(√(h/g)) t_2 −t_1 =(√((3h)/g))−((√((3h)/g))−(√(h/g)))=(√(h/g)) time from B to D=2(t_2 −t_1 )=2(√(h/g)) ⇒answer (c)](https://www.tinkutara.com/question/Q59913.png)
$${u}=\mathrm{2}\sqrt{{gh}} \\ $$$${from}\:{A}\:{to}\:{B}\:{in}\:{time}\:{t}_{\mathrm{1}} : \\ $$$${h}={u}\:\mathrm{sin}\:\theta\:{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:…\left({i}\right) \\ $$$${a}={u}\:\mathrm{cos}\:\theta\:{t}_{\mathrm{1}} \:\:\:\:…\left({ii}\right) \\ $$$${from}\:{A}\:{to}\:{C}\:{in}\:{time}\:{t}_{\mathrm{2}} : \\ $$$${a}+{h}={u}\:\mathrm{cos}\:\theta\:{t}_{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${u}\:\mathrm{sin}\:\theta−{gt}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{t}_{\mathrm{2}} =\frac{{u}\:\mathrm{sin}\:\theta}{{g}} \\ $$$$\left({iii}\right)−\left({ii}\right): \\ $$$${h}={u}\:\mathrm{cos}\:\theta\:\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right) \\ $$$${h}={u}\:\mathrm{cos}\:\theta\:\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−{t}_{\mathrm{1}} \right) \\ $$$$\Rightarrow{t}_{\mathrm{1}} =\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\:\:\:…\left({iv}\right) \\ $$$${put}\:\left({iv}\right)\:{into}\:\left({i}\right): \\ $$$${h}=\left[{u}\:\mathrm{sin}\:\theta\:−\frac{\mathrm{1}}{\mathrm{2}}{g}\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\right)\right]\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\right) \\ $$$${h}=\frac{\mathrm{1}}{\mathrm{2}{g}}\left({u}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\frac{{g}^{\mathrm{2}} {h}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\right) \\ $$$${h}=\frac{\mathrm{1}}{\mathrm{2}{g}}\left(\mathrm{4}{gh}\:\mathrm{sin}^{\mathrm{2}} \:\theta−\frac{{g}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{4}{gh}\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right) \\ $$$$\mathrm{1}=\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{1}=\mathrm{2}−\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{16}\:\mathrm{cos}^{\mathrm{4}} \:\theta−\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\theta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{3}}=\mathrm{60}° \\ $$$${t}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{{gh}}}{{g}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{3}{h}}{{g}}} \\ $$$${t}_{\mathrm{1}} =\frac{\mathrm{2}\sqrt{{gh}}}{{g}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{h}}{\mathrm{2}\sqrt{{gh}}×\frac{\mathrm{1}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{3}{h}}{{g}}}−\sqrt{\frac{{h}}{{g}}} \\ $$$${t}_{\mathrm{2}} −{t}_{\mathrm{1}} =\sqrt{\frac{\mathrm{3}{h}}{{g}}}−\left(\sqrt{\frac{\mathrm{3}{h}}{{g}}}−\sqrt{\frac{{h}}{{g}}}\right)=\sqrt{\frac{{h}}{{g}}} \\ $$$$ \\ $$$${time}\:{from}\:{B}\:{to}\:{D}=\mathrm{2}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)=\mathrm{2}\sqrt{\frac{{h}}{{g}}} \\ $$$$\Rightarrow{answer}\:\left({c}\right) \\ $$
Commented by rahul 19 last updated on 16/May/19

$${Thank}\:{You}\:{Sir}! \\ $$
