Question Number 59893 by aliesam last updated on 15/May/19
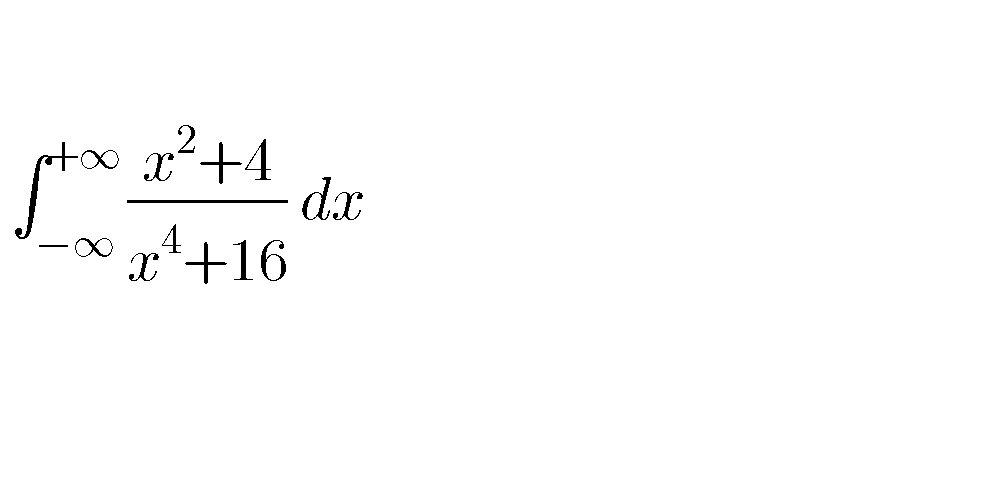
Commented by maxmathsup by imad last updated on 15/May/19

$${method}\:{using}\:{the}\:{formuae}\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:\:{if}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{4}}{{x}^{\mathrm{4}} \:+\mathrm{16}}\:\Rightarrow{I}\:=_{{x}=\mathrm{2}{t}} \:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{4}}{\mathrm{16}{t}^{\mathrm{4}} \:+\mathrm{16}}\:\left(\mathrm{2}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:+\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{t}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$${changement}\:\:\:{t}^{\mathrm{4}} \:={u}\:\:{give}\:{t}\:={u}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{\mathrm{4}}{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}^{\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${same}\:{changement}\:{give}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{I}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:+\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\:\frac{\mathrm{2}\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\Rightarrow\:\bigstar\:{I}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\bigstar \\ $$
Commented by malwaan last updated on 15/May/19

$${great}\:{sir} \\ $$$${but}\:;\:{can}\:{anyone}\:{solve}\:{it} \\ $$$${without}\:{using}\:{this}\:{formulae} \\ $$
Commented by maxmathsup by imad last updated on 16/May/19
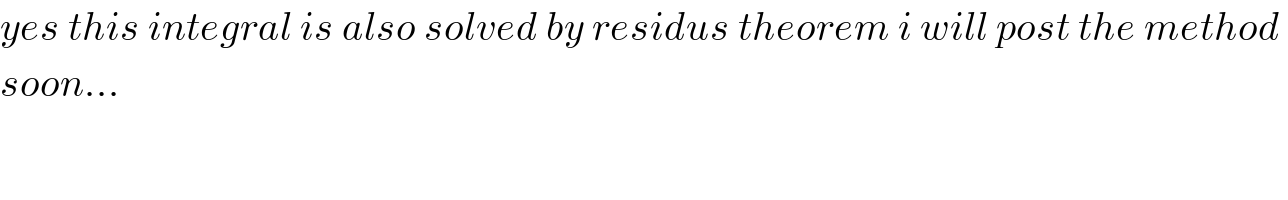
$${yes}\:{this}\:{integral}\:{is}\:{also}\:{solved}\:{by}\:{residus}\:{theorem}\:{i}\:{will}\:{post}\:{the}\:{method}\: \\ $$$${soon}… \\ $$
Commented by malwaan last updated on 16/May/19

$${thanks}\:{sir}\: \\ $$$${I}\:{am}\:{waiting}\:… \\ $$
Commented by maxmathsup by imad last updated on 17/May/19

$${residus}\:{method}\:{let}\:\:{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{4}}{{x}^{\mathrm{4}} \:+\mathrm{16}}{dx}\:\Rightarrow{A}=_{{x}=\mathrm{2}{t}} \:\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{4}}{\mathrm{16}\left({t}^{\mathrm{4}} \:+\mathrm{1}\right)}\mathrm{2}{dt} \\ $$$$\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:\:{let}\:{W}\left({z}\right)\:=\:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{4}} \:+\mathrm{1}}\:\:\:{poles}\:{of}\:{W}! \\ $$$${W}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)}\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:\:{so}\:{the}\:{poles}\:{of}\:{W} \\ $$$${are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:{and}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right)\:=\:\frac{{i}+\mathrm{1}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}+{i}}{\mathrm{4}{i}\:}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right)\:=\:\frac{−{i}+\mathrm{1}}{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\left(−\mathrm{2}{i}\right)}\:=\frac{\left(\mathrm{1}−{i}\right){e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\frac{\mathrm{1}+{i}}{\mathrm{4}{i}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:+\frac{\mathrm{1}−{i}}{\mathrm{4}{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right\}\:=\frac{\pi}{\mathrm{2}}\:\left(\:\mathrm{2}{Re}\left(\mathrm{1}+{i}\right){e}^{−\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$$=\pi\:{Re}\left\{\:\left(\mathrm{1}+{i}\right){e}^{−\frac{{i}\pi}{\mathrm{4}}} \right\}\:{but}\:\:\left(\mathrm{1}+{i}\right){e}^{−{i}\frac{\pi}{\mathrm{4}}} \:=\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:=\sqrt{\mathrm{2}}\:\Rightarrow\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\:=\pi\sqrt{\mathrm{2}\:}\:\Rightarrow \\ $$$$\mathrm{2}{A}\:=\pi\sqrt{\mathrm{2}}\:\Rightarrow\:{A}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\:{A}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:. \\ $$
Commented by malwaan last updated on 18/May/19
$${Thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
Commented by maxmathsup by imad last updated on 18/May/19
$${you}\:{are}\:{welcome}. \\ $$
