Question Number 60010 by naka3546 last updated on 17/May/19
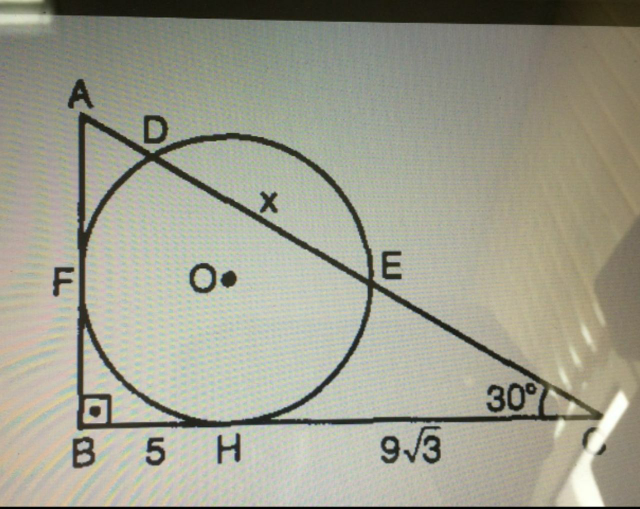
Commented by naka3546 last updated on 17/May/19
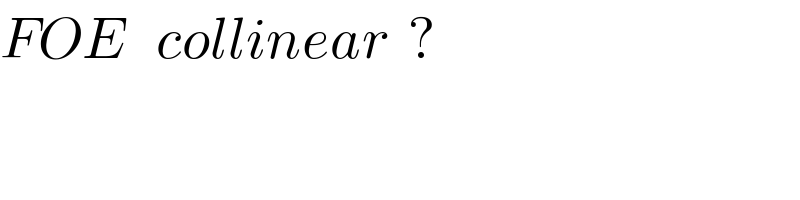
$${FOE}\:\:\:{collinear}\:\:? \\ $$
Answered by tanmay last updated on 17/May/19
![CD×CE=CH^2 (CE+ED)×CE=243 circle(x−5)^2 +(y−5)^2 =5^2 BC=5+9(√3) tan30^o =((AB)/(BC))→AB=(5+9(√3) )×(1/( (√3))) eqn AC (x/(5+9(√3)))+((y(√3) )/((5+9(√3) )))=1 x+y(√3) −(5+9(√3) )=0 distance from (5,5) to st line AC is d(say) d=∣((5+5(√3) −5−9(√3))/( (√(1^2 +((√3) )^2 ))))∣=2(√3) (2(√3) )^2 +(((DE)/2))^2 =5^2 DE^2 =52 DE=2(√(13)) (CE+DE)×CE=243 (CE+2(√(13)) )×CE=243 CE^2 +2×CE×(√(13)) +13=256 (CE+(√(13)) )^2 =16^2 CE=16+(√(13)) ,16−(√(13)) let coordinate of E(a,b) sin30^o =(b/(16+(√(13)))) [or(b/(16−(√(13))))] b=(1/2)(16+(√(13)) ) or b=(1/2)(16−(√(13)) ) cos30^o =((√3)/2)=(a/(16+(√(13)))) a=((√3)/2)(16+(√(13 )) ) eqn of st line FO is y=5 but {((√3)/2)(16+(√(13)) ),((16+(√(13)))/2)) do not satisy eqn y=5 so F,O,E not colliniar... pls check mistake if any](https://www.tinkutara.com/question/Q60018.png)
$${CD}×{CE}={CH}^{\mathrm{2}} \\ $$$$\left({CE}+{ED}\right)×{CE}=\mathrm{243} \\ $$$${circle}\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${BC}=\mathrm{5}+\mathrm{9}\sqrt{\mathrm{3}}\: \\ $$$${tan}\mathrm{30}^{{o}} =\frac{{AB}}{{BC}}\rightarrow{AB}=\left(\mathrm{5}+\mathrm{9}\sqrt{\mathrm{3}}\:\right)×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${eqn}\:{AC}\:\:\:\frac{{x}}{\mathrm{5}+\mathrm{9}\sqrt{\mathrm{3}}}+\frac{{y}\sqrt{\mathrm{3}}\:}{\left(\mathrm{5}+\mathrm{9}\sqrt{\mathrm{3}}\:\right)}=\mathrm{1} \\ $$$${x}+{y}\sqrt{\mathrm{3}}\:−\left(\mathrm{5}+\mathrm{9}\sqrt{\mathrm{3}}\:\right)=\mathrm{0} \\ $$$${distance}\:{from}\:\left(\mathrm{5},\mathrm{5}\right)\:{to}\:{st}\:{line}\:{AC}\:{is}\:{d}\left({say}\right) \\ $$$${d}=\mid\frac{\mathrm{5}+\mathrm{5}\sqrt{\mathrm{3}}\:−\mathrm{5}−\mathrm{9}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }}\mid=\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\left(\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} +\left(\frac{{DE}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${DE}^{\mathrm{2}} =\mathrm{52} \\ $$$${DE}=\mathrm{2}\sqrt{\mathrm{13}}\: \\ $$$$\left({CE}+{DE}\right)×{CE}=\mathrm{243} \\ $$$$\left({CE}+\mathrm{2}\sqrt{\mathrm{13}}\:\right)×{CE}=\mathrm{243} \\ $$$${CE}^{\mathrm{2}} +\mathrm{2}×{CE}×\sqrt{\mathrm{13}}\:+\mathrm{13}=\mathrm{256} \\ $$$$\left({CE}+\sqrt{\mathrm{13}}\:\right)^{\mathrm{2}} =\mathrm{16}^{\mathrm{2}} \\ $$$${CE}=\mathrm{16}+\sqrt{\mathrm{13}}\:,\mathrm{16}−\sqrt{\mathrm{13}}\: \\ $$$${let}\:{coordinate}\:{of}\:{E}\left({a},{b}\right) \\ $$$${sin}\mathrm{30}^{{o}} =\frac{{b}}{\mathrm{16}+\sqrt{\mathrm{13}}}\:\:\left[{or}\frac{{b}}{\mathrm{16}−\sqrt{\mathrm{13}}}\right] \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{16}+\sqrt{\mathrm{13}}\:\right)\:\:{or}\:\:{b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{16}−\sqrt{\mathrm{13}}\:\:\right) \\ $$$${cos}\mathrm{30}^{{o}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{{a}}{\mathrm{16}+\sqrt{\mathrm{13}}} \\ $$$${a}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{16}+\sqrt{\mathrm{13}\:}\:\right) \\ $$$${eqn}\:{of}\:{st}\:{line}\:{FO}\:{is}\:{y}=\mathrm{5} \\ $$$${but}\:\left\{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{16}+\sqrt{\mathrm{13}}\:\right),\frac{\mathrm{16}+\sqrt{\mathrm{13}}}{\mathrm{2}}\right)\:{do}\:{not}\:{satisy}\:{eqn} \\ $$$${y}=\mathrm{5}\: \\ $$$${so}\:{F},{O},{E}\:{not}\:{colliniar}… \\ $$$${pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
