Question Number 60054 by bhanukumarb2@gmail.com last updated on 17/May/19
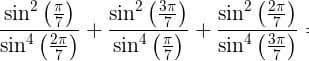
Commented by bhanukumarb2@gmail.com last updated on 17/May/19
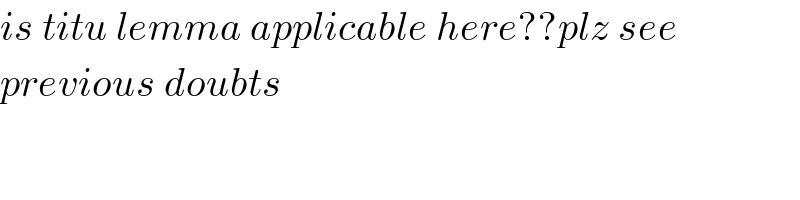
$${is}\:{titu}\:{lemma}\:{applicable}\:{here}??{plz}\:{see} \\ $$$${previous}\:{doubts} \\ $$
Answered by tanmay last updated on 17/May/19
![8x^3 −4x^2 −4x+1=0 roots are cos((π/7)),cos(((3π)/7)),cos(((5π)/7)) now cos(((5π)/7))=cos(((7π−2π)/7))=cos(π−((2π)/7))=−cos(((2π)/7)) let c_1 =cos((π/7)) so s_1 =sin((π/7)) c_2 =cos(((2π)/7)) s_2 =sin(((2π)/7)) c_3 =cos(((3π)/7)) s_3 =(((3π)/7)) ★★c_5 =cos(((5π)/7))=−cos(((2π)/7))=−c_2 ★★ our task to find value of (s_1 ^2 /s_2 ^4 )+(s_3 ^2 /s_1 ^4 )+(s_2 ^2 /s_3 ^4 ) 8x^3 −4x^2 −4x+1=0 roots are c_1 ,c_3 ,c_5 [note c_5 =−c_2 ] c_1 +c_3 +c_5 =((−(−4))/8)=(1/2) c_1 −c_2 +c_3 =(1/2) c_1 c_3 +c_1 c_5 +c_3 c_5 =((−4)/8) c_1 c_3 +c_1 (−c_2 )+c_3 (−c_2 )=((−4)/8) c_1 c_3 −c_1 c_2 −c_3 c_2 =((−1)/2) c_1 c_3 c_5 =((−1)/8) c_1 ×c_3 ×−c_2 =((−1)/8) c_1 c_2 c_3 =(1/8) (s_1 ^2 /s_2 ^4 )+(s_3 ^2 /s_1 ^4 )+(s_2 ^2 /s_3 ^4 )=((s_1 ^2 (s_1 ^4 s_3 ^4 )+s_3 ^2 (s_2 ^4 s_3 ^4 )+s_2 ^2 (s_2 ^4 s_1 ^4 ))/((s_1 s_2 s_3 )^4 )) =((s_1 ^6 s_3 ^4 +s_3 ^6 s_2 ^4 +s_2 ^6 s_1 ^(4i) )/((s_1 s_2 s_3 )^4 )) 8c^3 −4c^2 −4c+1=0 c^2 +s^2 =1 8(1−s^2 )(√(1−s^2 )) −4(1−s^2 )−4((√(1−s^2 )))+1=0 4×(√(1−s^2 )) (2−2s^2 −1)=4(1−s^2 )−1 4×(√(1−s^2 )) (1−2s^2 )=(3−4s^2 ) 16(1−s^2 )(1−4s^2 +4s^4 )=9−24s^2 +16s^4 16(1−4s^2 +4s^4 −s^2 +4s^4 −4s^6 )=9−24s^2 +16s^4 −64s^6 +128s^4 −80s^2 +16−16s^4 +24s^2 −9=0 −64s^6 +112s^4 −53s^2 +7=0 if s^2 =t −64t^3 +112t^2 −53t+7=0 s_1 ^2 +s_2 ^2 +s_3 ^2 =((112)/(64)) s_1 ^2 s_2 ^2 +s_1 ^2 s_3 ^2 +s_2 ^2 s_3 ^2 =((53)/(64)) s_1 ^2 s_2 ^2 s_3 ^2 =(7/(64)) wait i am trying...](https://www.tinkutara.com/question/Q60087.png)
$$\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$${roots}\:{are}\:{cos}\left(\frac{\pi}{\mathrm{7}}\right),{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right),{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right) \\ $$$${now}\:{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right)={cos}\left(\frac{\mathrm{7}\pi−\mathrm{2}\pi}{\mathrm{7}}\right)={cos}\left(\pi−\frac{\mathrm{2}\pi}{\mathrm{7}}\right)=−{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right) \\ $$$${let}\:{c}_{\mathrm{1}} ={cos}\left(\frac{\pi}{\mathrm{7}}\right)\:\:\:{so}\:{s}_{\mathrm{1}} ={sin}\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$${c}_{\mathrm{2}} ={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:\:\:{s}_{\mathrm{2}} ={sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right) \\ $$$${c}_{\mathrm{3}} ={cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:\:\:\:{s}_{\mathrm{3}} =\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right) \\ $$$$\bigstar\bigstar{c}_{\mathrm{5}} ={cos}\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right)=−{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)=−{c}_{\mathrm{2}} \bigstar\bigstar \\ $$$${our}\:{task}\:{to}\:{find}\:{value}\:{of} \\ $$$$\frac{{s}_{\mathrm{1}} ^{\mathrm{2}} }{{s}_{\mathrm{2}} ^{\mathrm{4}} }+\frac{{s}_{\mathrm{3}} ^{\mathrm{2}} }{{s}_{\mathrm{1}} ^{\mathrm{4}} }+\frac{{s}_{\mathrm{2}} ^{\mathrm{2}} }{{s}_{\mathrm{3}} ^{\mathrm{4}} } \\ $$$$\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$${roots}\:{are}\:{c}_{\mathrm{1}} ,{c}_{\mathrm{3}} ,{c}_{\mathrm{5}} \:\:\:\left[{note}\:{c}_{\mathrm{5}} =−{c}_{\mathrm{2}} \right] \\ $$$${c}_{\mathrm{1}} +{c}_{\mathrm{3}} +{c}_{\mathrm{5}} =\frac{−\left(−\mathrm{4}\right)}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} −{c}_{\mathrm{2}} +{c}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} {c}_{\mathrm{3}} +{c}_{\mathrm{1}} {c}_{\mathrm{5}} +{c}_{\mathrm{3}} {c}_{\mathrm{5}} =\frac{−\mathrm{4}}{\mathrm{8}} \\ $$$${c}_{\mathrm{1}} {c}_{\mathrm{3}} +{c}_{\mathrm{1}} \left(−{c}_{\mathrm{2}} \right)+{c}_{\mathrm{3}} \left(−{c}_{\mathrm{2}} \right)=\frac{−\mathrm{4}}{\mathrm{8}} \\ $$$${c}_{\mathrm{1}} {c}_{\mathrm{3}} −{c}_{\mathrm{1}} {c}_{\mathrm{2}} −{c}_{\mathrm{3}} {c}_{\mathrm{2}} =\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} {c}_{\mathrm{3}} {c}_{\mathrm{5}} =\frac{−\mathrm{1}}{\mathrm{8}} \\ $$$${c}_{\mathrm{1}} ×{c}_{\mathrm{3}} ×−{c}_{\mathrm{2}} =\frac{−\mathrm{1}}{\mathrm{8}} \\ $$$${c}_{\mathrm{1}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\frac{{s}_{\mathrm{1}} ^{\mathrm{2}} }{{s}_{\mathrm{2}} ^{\mathrm{4}} }+\frac{{s}_{\mathrm{3}} ^{\mathrm{2}} }{{s}_{\mathrm{1}} ^{\mathrm{4}} }+\frac{{s}_{\mathrm{2}} ^{\mathrm{2}} }{{s}_{\mathrm{3}} ^{\mathrm{4}} }=\frac{{s}_{\mathrm{1}} ^{\mathrm{2}} \left({s}_{\mathrm{1}} ^{\mathrm{4}} {s}_{\mathrm{3}} ^{\mathrm{4}} \right)+{s}_{\mathrm{3}} ^{\mathrm{2}} \left({s}_{\mathrm{2}} ^{\mathrm{4}} {s}_{\mathrm{3}} ^{\mathrm{4}} \right)+{s}_{\mathrm{2}} ^{\mathrm{2}} \left({s}_{\mathrm{2}} ^{\mathrm{4}} {s}_{\mathrm{1}} ^{\mathrm{4}} \right)}{\left({s}_{\mathrm{1}} {s}_{\mathrm{2}} {s}_{\mathrm{3}} \right)^{\mathrm{4}} } \\ $$$$=\frac{{s}_{\mathrm{1}} ^{\mathrm{6}} {s}_{\mathrm{3}} ^{\mathrm{4}} +{s}_{\mathrm{3}} ^{\mathrm{6}} {s}_{\mathrm{2}} ^{\mathrm{4}} +{s}_{\mathrm{2}} ^{\mathrm{6}} {s}_{\mathrm{1}} ^{\mathrm{4}{i}} }{\left({s}_{\mathrm{1}} {s}_{\mathrm{2}} {s}_{\mathrm{3}} \right)^{\mathrm{4}} } \\ $$$$ \\ $$$$\mathrm{8}{c}^{\mathrm{3}} −\mathrm{4}{c}^{\mathrm{2}} −\mathrm{4}{c}+\mathrm{1}=\mathrm{0} \\ $$$${c}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{8}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\:−\mathrm{4}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)−\mathrm{4}\left(\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\right)+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4}×\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\:\left(\mathrm{2}−\mathrm{2}{s}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{4}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)−\mathrm{1} \\ $$$$\mathrm{4}×\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\:\left(\mathrm{1}−\mathrm{2}{s}^{\mathrm{2}} \right)=\left(\mathrm{3}−\mathrm{4}{s}^{\mathrm{2}} \right) \\ $$$$\mathrm{16}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{4}{s}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{4}} \right)=\mathrm{9}−\mathrm{24}{s}^{\mathrm{2}} +\mathrm{16}{s}^{\mathrm{4}} \\ $$$$\mathrm{16}\left(\mathrm{1}−\mathrm{4}{s}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{4}} −{s}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{4}} −\mathrm{4}{s}^{\mathrm{6}} \right)=\mathrm{9}−\mathrm{24}{s}^{\mathrm{2}} +\mathrm{16}{s}^{\mathrm{4}} \\ $$$$−\mathrm{64}{s}^{\mathrm{6}} +\mathrm{128}{s}^{\mathrm{4}} −\mathrm{80}{s}^{\mathrm{2}} +\mathrm{16}−\mathrm{16}{s}^{\mathrm{4}} +\mathrm{24}{s}^{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$$−\mathrm{64}{s}^{\mathrm{6}} +\mathrm{112}{s}^{\mathrm{4}} −\mathrm{53}{s}^{\mathrm{2}} +\mathrm{7}=\mathrm{0} \\ $$$${if}\:{s}^{\mathrm{2}} ={t} \\ $$$$−\mathrm{64}{t}^{\mathrm{3}} +\mathrm{112}{t}^{\mathrm{2}} −\mathrm{53}{t}+\mathrm{7}=\mathrm{0} \\ $$$${s}_{\mathrm{1}} ^{\mathrm{2}} +{s}_{\mathrm{2}} ^{\mathrm{2}} +{s}_{\mathrm{3}} ^{\mathrm{2}} =\frac{\mathrm{112}}{\mathrm{64}} \\ $$$${s}_{\mathrm{1}} ^{\mathrm{2}} {s}_{\mathrm{2}} ^{\mathrm{2}} +{s}_{\mathrm{1}} ^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} +{s}_{\mathrm{2}} ^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} =\frac{\mathrm{53}}{\mathrm{64}} \\ $$$${s}_{\mathrm{1}} ^{\mathrm{2}} {s}_{\mathrm{2}} ^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{64}} \\ $$$${wait}\:{i}\:{am}\:{trying}… \\ $$
Commented by bhanukumarb2@gmail.com last updated on 17/May/19
$${thanku}\:{sir}\:{i}\:{will}\:{do}\:{next}\:{part}\:{thanku} \\ $$
Commented by otchereabdullai@gmail.com last updated on 17/May/19
$$\mathrm{Brilliant}\:\mathrm{prof}\:\mathrm{Tanmay} \\ $$
