Question Number 60058 by ajfour last updated on 17/May/19

Commented by ajfour last updated on 17/May/19
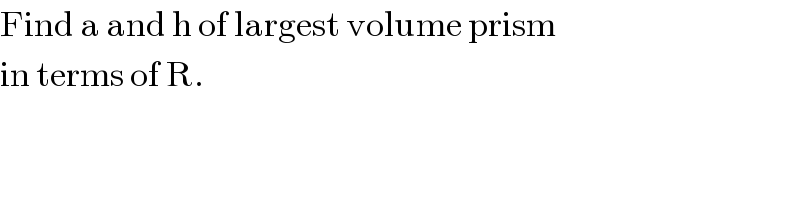
$$\mathrm{Find}\:\mathrm{a}\:\mathrm{and}\:\mathrm{h}\:\mathrm{of}\:\mathrm{largest}\:\mathrm{volume}\:\mathrm{prism} \\ $$$$\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{R}. \\ $$
Answered by mr W last updated on 17/May/19

Commented by mr W last updated on 17/May/19

$${r}=\sqrt{{R}^{\mathrm{2}} −\frac{{h}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${a}=\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{r}=\sqrt{\mathrm{3}\left({R}^{\mathrm{2}} −\frac{{h}^{\mathrm{2}} }{\mathrm{4}}\right)} \\ $$$${A}_{{base}} =\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\left({R}^{\mathrm{2}} −\frac{{h}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${V}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}\left(\mathrm{4}{R}^{\mathrm{2}} −{h}^{\mathrm{2}} \right){h} \\ $$$$\frac{{dV}}{{dh}}=\mathrm{0}\:\Rightarrow\mathrm{4}{R}^{\mathrm{2}} −\mathrm{3}{h}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{h}=\frac{\mathrm{2}{R}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{a}=\sqrt{\mathrm{2}}{R} \\ $$
Commented by ajfour last updated on 17/May/19
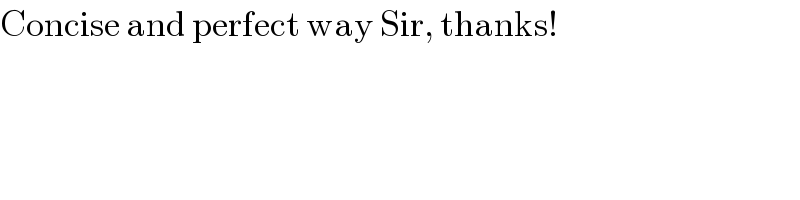
$$\mathrm{Concise}\:\mathrm{and}\:\mathrm{perfect}\:\mathrm{way}\:\mathrm{Sir},\:\mathrm{thanks}! \\ $$
Commented by ajfour last updated on 17/May/19
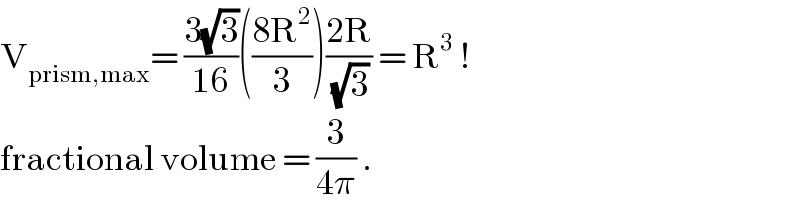
$$\mathrm{V}_{\mathrm{prism},\mathrm{max}} =\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}\left(\frac{\mathrm{8R}^{\mathrm{2}} }{\mathrm{3}}\right)\frac{\mathrm{2R}}{\:\sqrt{\mathrm{3}}}\:=\:\mathrm{R}^{\mathrm{3}} \:! \\ $$$$\mathrm{fractional}\:\mathrm{volume}\:=\:\frac{\mathrm{3}}{\mathrm{4}\pi}\:. \\ $$
