Question Number 60088 by ajfour last updated on 17/May/19

Commented by ajfour last updated on 17/May/19

$$\mathrm{Only}\:\mathrm{hemisphere}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{R}\:\mathrm{is}\:\mathrm{grassy}, \\ $$$$\mathrm{and}\:\mathrm{occupies}\:\mathrm{central}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{square}\:\mathrm{field}\:\mathrm{of}\:\mathrm{side}\:\mathrm{a}>\:\mathrm{2R}. \\ $$$$\mathrm{A}\:\mathrm{goat}\:\mathrm{tied}\:\mathrm{at}\:\mathrm{front}\:\mathrm{right}\:\mathrm{corner} \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{rope}\:\mathrm{of}\:\mathrm{length}\:{l}=\:\frac{{a}}{\mathrm{2}}\:, \\ $$$$\mathrm{can}\:\mathrm{graze}\:\mathrm{max}.\:\mathrm{what}\:\mathrm{area}\:\mathrm{of}\:\mathrm{grass}? \\ $$$$\left(\mathrm{express}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a},\mathrm{and}\:\mathrm{R}.\right. \\ $$
Answered by mr W last updated on 17/May/19

Commented by mr W last updated on 17/May/19
![d=(((√2)a)/2) (√(R^2 −r^2 ))=d−(√(l^2 −r^2 )) R^2 −r^2 =d^2 +l^2 −r^2 −2d(√(l^2 −r^2 )) d^2 +l^2 −R^2 =2d(√(l^2 −r^2 )) (d^2 +l^2 −R^2 )^2 =4d^2 (l^2 −r^2 ) r=(√(l^2 −(((d^2 +l^2 −R^2 )/(2d)))^2 )) surface area of spherical cap: A_(cap) =2πR(R−(√(R^2 −r^2 ))) due to hemisphere the grass area is half of the spherical cap: A_g =πR(R−(√(R^2 −r^2 )))=πR[R−(√(R^2 −l^2 +(((d^2 +l^2 −R^2 )/(2d)))^2 ))] =πR[R−(√(R^2 −l^2 +(1/8)(((a^2 +2l^2 −2R^2 )/a))^2 ))]](https://www.tinkutara.com/question/Q60102.png)
$${d}=\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}} \\ $$$$\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }={d}−\sqrt{{l}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} −{r}^{\mathrm{2}} ={d}^{\mathrm{2}} +{l}^{\mathrm{2}} −{r}^{\mathrm{2}} −\mathrm{2}{d}\sqrt{{l}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${d}^{\mathrm{2}} +{l}^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{2}{d}\sqrt{{l}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\left({d}^{\mathrm{2}} +{l}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{d}^{\mathrm{2}} \left({l}^{\mathrm{2}} −{r}^{\mathrm{2}} \right) \\ $$$${r}=\sqrt{{l}^{\mathrm{2}} −\left(\frac{{d}^{\mathrm{2}} +{l}^{\mathrm{2}} −{R}^{\mathrm{2}} }{\mathrm{2}{d}}\right)^{\mathrm{2}} } \\ $$$${surface}\:{area}\:{of}\:{spherical}\:{cap}: \\ $$$${A}_{{cap}} =\mathrm{2}\pi{R}\left({R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right) \\ $$$${due}\:{to}\:{hemisphere}\:{the}\:{grass}\:{area}\:{is} \\ $$$${half}\:{of}\:{the}\:{spherical}\:{cap}: \\ $$$${A}_{{g}} =\pi{R}\left({R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)=\pi{R}\left[{R}−\sqrt{{R}^{\mathrm{2}} −{l}^{\mathrm{2}} +\left(\frac{{d}^{\mathrm{2}} +{l}^{\mathrm{2}} −{R}^{\mathrm{2}} }{\mathrm{2}{d}}\right)^{\mathrm{2}} }\right] \\ $$$$=\pi{R}\left[{R}−\sqrt{{R}^{\mathrm{2}} −{l}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{{a}^{\mathrm{2}} +\mathrm{2}{l}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} }{{a}}\right)^{\mathrm{2}} }\right] \\ $$
Commented by ajfour last updated on 17/May/19

$$\mathrm{Hope}\:\mathrm{i}\:\mathrm{shall}\:\mathrm{follow}.. \\ $$$$\mathrm{you}'\mathrm{re}\:\mathrm{amazingly}\:\mathrm{quick}\:\mathrm{my}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 17/May/19
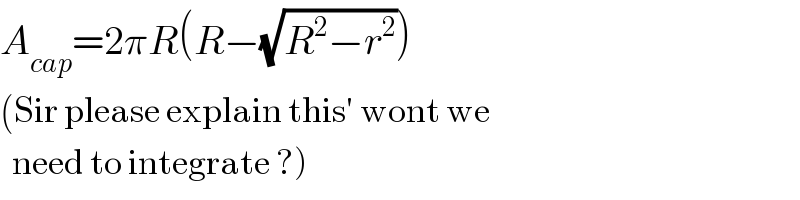
$${A}_{{cap}} =\mathrm{2}\pi{R}\left({R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right) \\ $$$$\left(\mathrm{Sir}\:\mathrm{please}\:\mathrm{explain}\:\mathrm{this}'\:\mathrm{wont}\:\mathrm{we}\right. \\ $$$$\left.\:\:\mathrm{need}\:\mathrm{to}\:\mathrm{integrate}\:?\right) \\ $$
Commented by mr W last updated on 17/May/19
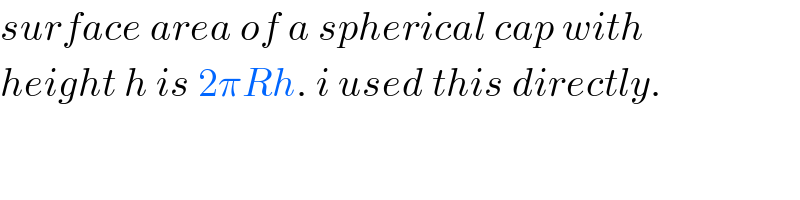
$${surface}\:{area}\:{of}\:{a}\:{spherical}\:{cap}\:{with} \\ $$$${height}\:{h}\:{is}\:\mathrm{2}\pi{Rh}.\:{i}\:{used}\:{this}\:{directly}. \\ $$
Commented by mr W last updated on 17/May/19

Commented by otchereabdullai@gmail.com last updated on 17/May/19
$$\mathrm{I}\:\mathrm{salute}\:\mathrm{you}\:\mathrm{prof}\:\mathrm{W} \\ $$
