Question Number 60121 by rahul 19 last updated on 18/May/19

Commented by rahul 19 last updated on 18/May/19
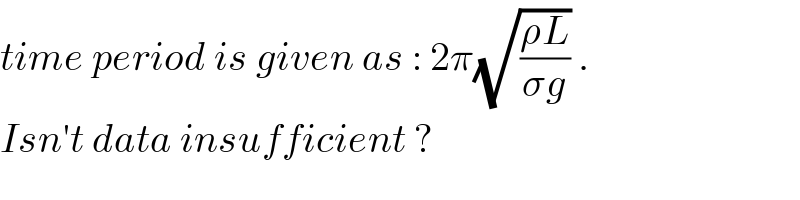
$${time}\:{period}\:{is}\:{given}\:{as}\::\:\mathrm{2}\pi\sqrt{\frac{\rho{L}}{\sigma{g}}}\:. \\ $$$${Isn}'{t}\:{data}\:{insufficient}\:? \\ $$
Commented by mr W last updated on 18/May/19

$${data}\:{is}\:{enough}. \\ $$$${answer}\:{a}\:{is}\:{correct}. \\ $$
Commented by mr W last updated on 18/May/19

$${for}\:{an}\:{object}\:{with}\:{uniform}\:{cross}\:{section}, \\ $$$${to}\:{determine}\:{the}\:{frequency}\:{or}\:{time} \\ $$$${period}\:{of}\:{its}\:{vertical}\:{oscillation}\:{in}\:{a}\:{liquid}, \\ $$$${we}\:\boldsymbol{{only}}\:{need}\:{to}\:{know}\:{how}\:{much}\:{of} \\ $$$${it}\:{is}\:{immersed}\:{when}\:{it}\:{is}\:{floating}\:{in} \\ $$$${the}\:{liquid}. \\ $$$${f}=\frac{\mathrm{1}}{\mathrm{2}\pi}\sqrt{\frac{{g}}{{L}_{{w}} }} \\ $$$${T}=\mathrm{2}\pi\sqrt{\frac{{L}_{{w}} }{{g}}} \\ $$$${with}\:{L}_{{w}} ={depth}\:{immersed}\:{in}\:{liquid} \\ $$
Answered by mr W last updated on 18/May/19

$${let}\:{length}\:{of}\:{pole}={L},\:{cross}\:{section}={A} \\ $$$${length}\:{immersed}\:{in}\:{liquid}\:{when}\:{floating}={L}_{{w}} \\ $$$${density}\:{of}\:{pole}=\rho \\ $$$${density}\:{of}\:{liquid}=\rho_{{w}} \\ $$$${when}\:{floating}\Rightarrow{A}\rho_{{w}} {gL}_{{w}} ={A}\rho{gL}\Rightarrow\rho_{{w}} {L}_{{w}} =\rho{L} \\ $$$${T}=\mathrm{2}\pi\sqrt{\frac{{L}\rho}{\rho_{{w}} {g}}}=\mathrm{2}\pi\sqrt{\frac{\rho_{{w}} {L}_{{w}} }{\rho_{{w}} {g}}}=\mathrm{2}\pi\sqrt{\frac{{L}_{{w}} }{{g}}} \\ $$$$=\mathrm{2}\pi\sqrt{\frac{\mathrm{0}.\mathrm{8}}{\mathrm{9}.\mathrm{81}}}=\frac{\mathrm{3}.\mathrm{998}\pi}{\mathrm{7}}\approx\frac{\mathrm{4}\pi}{\mathrm{7}} \\ $$$$\Rightarrow{answer}\:{a} \\ $$
Commented by rahul 19 last updated on 19/May/19

$${thank}\:{you}\:{sir}. \\ $$
Answered by tanmay last updated on 18/May/19

$${wt}\:{of}\:{pole}={upthrust} \\ $$$${mg}=\pi{R}^{\mathrm{2}} {x}\rho_{{liquid}} {g} \\ $$$$\pi{R}^{\mathrm{2}} {h}\rho_{{pole}} {g}=\pi{R}^{\mathrm{2}} {x}\rho_{{liwuid}} {g} \\ $$$${h}={length}\:{of}\:{pole} \\ $$$${x}={submerged}\:{length}\:{of}\:{pole} \\ $$$${when}\:{pushed}\:{further}\:{by}\:\bigtriangleup{x} \\ $$$${then}\:{upthrust}>{wt}\:{of}\:{pole} \\ $$$${so}\:{restoring}\:{force} \\ $$$$=\pi{R}^{\mathrm{2}} \left({x}+\bigtriangleup{x}\right)\rho_{{liq}} {g}−\pi{R}^{\mathrm{2}} {h}\rho_{{pole}} {g} \\ $$$$=\pi{R}^{\mathrm{2}} {x}\rho_{{liq}} {g}−\pi{R}^{\mathrm{2}} {h}\rho_{{pole}} {g}+\pi{R}^{\mathrm{2}} .\bigtriangleup{x}.\rho_{{liq}} {g} \\ $$$$=\pi{R}^{\mathrm{2}} .\bigtriangleup{x}.\rho_{{liq}} {g} \\ $$$${accelaration}\left({w}^{\mathrm{2}} \bigtriangleup{x}\right) \\ $$$$=\frac{\pi{R}^{\mathrm{2}} .\bigtriangleup{x}.\rho_{{liq}} {g}}{\pi{R}^{\mathrm{2}} {h}\rho_{{pole}} } \\ $$$$=\frac{\rho_{{liq}} ×{g}}{\rho_{{pole}} ×{h}}×\bigtriangleup{x} \\ $$$${so}\:\:{w}^{\mathrm{2}} \bigtriangleup{x}=\frac{\rho_{{liq}} {g}}{\rho_{{pole}} {h}}×\bigtriangleup{x} \\ $$$$\frac{\mathrm{2}\pi}{{T}}=\sqrt{\frac{\rho_{{liq}} {g}}{\rho_{{pole}} {h}}}\: \\ $$$${T}=\mathrm{2}\pi×\sqrt{\frac{\rho_{{pole}} }{\rho_{{liq}} }×\frac{{h}}{{g}}}\: \\ $$$${in}\:{question}\:{no}\:{mention}\:{of}\:{value}\:{of} \\ $$$${density}\:{pole}\left(\rho_{{pole}} \right) \\ $$$${density}\:{liquid}\left(\rho_{\left.{liquid}\right)} \right. \\ $$$${length}\:{of}\:{pole}\left({h}\right) \\ $$$${now}..{from}\:{first}\:{eqn} \\ $$$${mg}=\pi{R}^{\mathrm{2}} {x}\rho_{{liq}} {g} \\ $$$$\pi{R}^{\mathrm{2}} {h}\rho_{{pole}} {g}=\pi{R}^{\mathrm{2}} {x}\rho_{{liq}} {g} \\ $$$${h}\rho_{{pole}} ={x}\rho_{{liquid}} \\ $$$$\frac{{h}\rho_{{pole}} }{\rho_{{liq}} }={x} \\ $$$${T}=\mathrm{2}\pi\sqrt{\frac{{x}}{{g}}}\: \\ $$$${given}\:{x}=\mathrm{80}{cm} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 19/May/19

$${thank}\:{u}\:{sir}. \\ $$
