Question Number 60133 by ajfour last updated on 18/May/19
Commented by ajfour last updated on 18/May/19

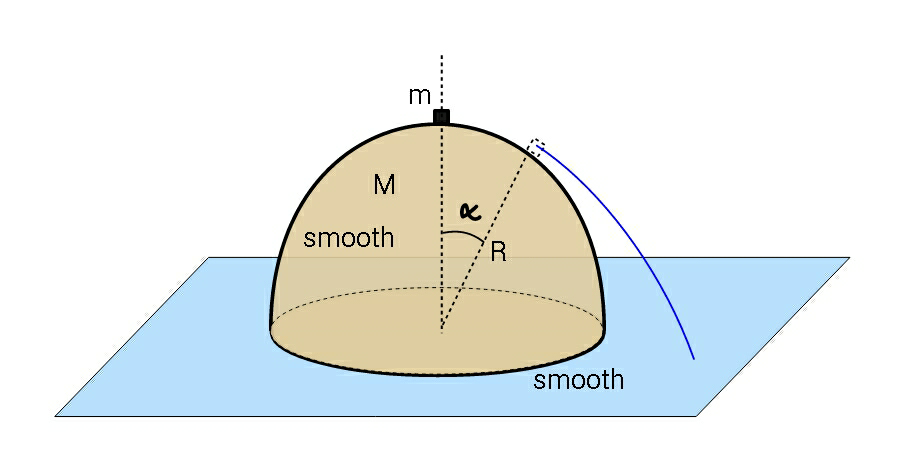
$$\mathrm{Find}\:\mathrm{angle}\:\alpha\:\mathrm{when}\:\mathrm{m}\:\mathrm{separates} \\ $$$$\mathrm{from}\:\mathrm{M}.\:\left(\mathrm{m}\:\mathrm{slides}\:\mathrm{down}\:\:\mathrm{from}\:\mathrm{top}\right. \\ $$$$\mathrm{of}\:\mathrm{M}\:,\:\mathrm{motion}\:\mathrm{being}\:\mathrm{initiated} \\ $$$$\left.\mathrm{somehow}\:\mathrm{with}\:\mathrm{a}\:\mathrm{slight}\:\mathrm{impulse}\right). \\ $$
Answered by mr W last updated on 22/May/19
![position of M: x_1 (+ve to right) velocity of M: v_1 acceleration of M: a ω=(dθ/dt) α=(dω/dt)=ω (dω/dθ) position of m: x_2 =x_1 +R sin θ y_2 =R cos θ v_(2x) =v_1 +R cos θ ω v_(2y) =−R sin θ ω a_(2x) =a_1 +R cos θ α−R sin θ ω^2 a_(2y) =−R sin θ α−R cos θ ω^2 ma_(2x) =N sin θ ⇒m(a_1 +R cos θ α−R sin θ ω^2 )=N sin θ ...(i) ma_(2y) =N cos θ−mg ⇒mR(sin θ α+cos θ ω^2 )=mg−N cos θ ...(ii) Ma_1 =−N sin θ ...(iii) ⇒Rω((dω/dθ) cos θ−ω sin θ)=(1+(m/M))[g−Rω(sin θ (dω/dθ)+ω cos θ )] tan θ with μ=(m/M) ⇒ω (dω/dθ)=((sin θ)/(1+μ sin^2 θ))[(1+μ)(g/R)−μω^2 cos θ] ⇒(dω^2 /dθ)=((2 sin θ)/(1+μ sin^2 θ))[(1+μ)(g/R)−μω^2 cos θ] with Φ=ω^2 ⇒(dΦ/dθ)+((μ sin 2θ)/(1+μ sin^2 θ))Φ=((2(1+μ)g)/R)×((sin θ)/(1+μ sin^2 θ)) ω=(√Φ)=f(θ) ... but not possible to solve.... try ing an other way: the CoM of both masses should be unchanged in horizontal direction during the motion, because no external force is acting in horizontal direction. −x_1 M=(x_1 +R sin θ)m ⇒−v_1 M=(v_1 +R cos θ ω)m ⇒v_1 =−((mR cos θ ω)/(m+M))=−((μR cos θ ω)/(1+μ)) ⇒a_1 =((μR)/(1+μ))(sin θ ω^2 −cos θ α) (1/2)Mv_1 ^2 +(1/2)m(v_(2x) ^2 +v_(2y) ^2 )=mgR(1−cos θ) v_1 ^2 +μ(v_(2x) ^2 +v_(2y) ^2 )=2gμR(1−cos θ) (1+μ)v_1 ^2 +2μRω cos θ v_1 +μR^2 ω^2 =2gμR(1−cos θ) −((μ^2 R^2 cos^2 θ ω^2 )/(1+μ))+μR^2 ω^2 =2gμR(1−cos θ) (((1+μ sin^2 θ)/(1+μ)))Rω^2 =2g(1−cos θ) ⇒ω^2 =((2g(1+μ)(1−cos θ))/(R(1+μ sin^2 θ))) ⇒2ωα=((2g(1+μ))/R){((sin θ)/(1+μ sin^2 θ))−(((1−cos θ)2μ sin θ cos θ)/((1+μ sin^2 θ)^2 ))}ω ⇒α=((g(1+μ) sin θ)/(R(1+μ sin^2 θ)^2 )){1+μ sin^2 θ−(1−cos θ)2μcos θ} ⇒α=((g(1+μ) sin θ)/(R(1+μ sin^2 θ)^2 )){1+μ(1−cos θ)^2 } N=−((Ma_1 )/(sin θ))=−((μRM)/((1+μ)sin θ))(sin θ ω^2 −cos θ α) N=−((μRM)/((1+μ)sin θ)){((2g(1+μ)sin θ(1−cos θ))/(R(1+μ sin^2 θ)))−((g(1+μ) sin θ cos θ [1+μ(1−cos θ)^2 ])/(R(1+μ sin^2 θ)^2 ))} N=−((μMg)/((1+μ sin^2 θ)^2 )){2(1−cos θ)(1+μ sin^2 θ)−cos θ [1+μ(1−cos θ)^2 ]} N=−((μMg)/((1+μ sin^2 θ)^2 )){2−3cos θ+μ(2+cos θ)(1−cos θ)^2 } ⇒(N/(Mg))=((μ[3cos θ−μ(2+cos θ)(1−cos θ)^2 −2])/((1+μ sin^2 θ)^2 )) for N=0: 2−3cos θ+μ(2+cos θ)(1−cos θ)^2 =0 2−3cos θ+μ(2+cos θ)(1−2cos θ+cos^2 θ)=0 ⇒(μ/(1+μ)) cos^3 θ−3 cos θ+2=0 ⇒λ cos^3 α−3 cos α+2=0 ⇒α=cos^(−1) {((((√(1−λ))−1)/λ))^(1/3) −((((√(1−λ))+1)/λ))^(1/3) }](https://www.tinkutara.com/question/Q60157.png)
$${position}\:{of}\:{M}:\:{x}_{\mathrm{1}} \:\left(+{ve}\:{to}\:{right}\right) \\ $$$${velocity}\:{of}\:{M}:\:{v}_{\mathrm{1}} \\ $$$${acceleration}\:{of}\:{M}:\:{a} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\omega\:\frac{{d}\omega}{{d}\theta} \\ $$$${position}\:{of}\:{m}: \\ $$$${x}_{\mathrm{2}} ={x}_{\mathrm{1}} +{R}\:\mathrm{sin}\:\theta \\ $$$${y}_{\mathrm{2}} ={R}\:\mathrm{cos}\:\theta \\ $$$${v}_{\mathrm{2}{x}} ={v}_{\mathrm{1}} +{R}\:\mathrm{cos}\:\theta\:\omega \\ $$$${v}_{\mathrm{2}{y}} =−{R}\:\mathrm{sin}\:\theta\:\omega \\ $$$${a}_{\mathrm{2}{x}} ={a}_{\mathrm{1}} +{R}\:\mathrm{cos}\:\theta\:\alpha−{R}\:\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} \\ $$$${a}_{\mathrm{2}{y}} =−{R}\:\mathrm{sin}\:\theta\:\alpha−{R}\:\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} \\ $$$${ma}_{\mathrm{2}{x}} ={N}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{m}\left({a}_{\mathrm{1}} +{R}\:\mathrm{cos}\:\theta\:\alpha−{R}\:\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} \right)={N}\:\mathrm{sin}\:\theta\:\:…\left({i}\right) \\ $$$${ma}_{\mathrm{2}{y}} ={N}\:\mathrm{cos}\:\theta−{mg} \\ $$$$\Rightarrow{mR}\left(\mathrm{sin}\:\theta\:\alpha+\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} \right)={mg}−{N}\:\mathrm{cos}\:\theta\:\:…\left({ii}\right) \\ $$$${Ma}_{\mathrm{1}} =−{N}\:\mathrm{sin}\:\theta\:\:…\left({iii}\right) \\ $$$$\Rightarrow{R}\omega\left(\frac{{d}\omega}{{d}\theta}\:\mathrm{cos}\:\theta−\omega\:\mathrm{sin}\:\theta\right)=\left(\mathrm{1}+\frac{{m}}{{M}}\right)\left[{g}−{R}\omega\left(\mathrm{sin}\:\theta\:\frac{{d}\omega}{{d}\theta}+\omega\:\mathrm{cos}\:\theta\:\right)\right]\:\mathrm{tan}\:\theta\: \\ $$$${with}\:\mu=\frac{{m}}{{M}} \\ $$$$\Rightarrow\omega\:\frac{{d}\omega}{{d}\theta}=\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}\left[\left(\mathrm{1}+\mu\right)\frac{{g}}{{R}}−\mu\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right] \\ $$$$\Rightarrow\frac{{d}\omega^{\mathrm{2}} }{{d}\theta}=\frac{\mathrm{2}\:\mathrm{sin}\:\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}\left[\left(\mathrm{1}+\mu\right)\frac{{g}}{{R}}−\mu\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right] \\ $$$${with}\:\Phi=\omega^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{d}\Phi}{{d}\theta}+\frac{\mu\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}\Phi=\frac{\mathrm{2}\left(\mathrm{1}+\mu\right){g}}{{R}}×\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\omega=\sqrt{\Phi}={f}\left(\theta\right) \\ $$$$…\:{but}\:{not}\:{possible}\:{to}\:{solve}…. \\ $$$$ \\ $$$${try}\:{ing}\:{an}\:{other}\:{way}: \\ $$$${the}\:{CoM}\:{of}\:{both}\:{masses}\:{should}\:{be} \\ $$$${unchanged}\:{in}\:{horizontal}\:{direction} \\ $$$${during}\:{the}\:{motion},\:{because}\:{no}\:{external} \\ $$$${force}\:{is}\:{acting}\:{in}\:{horizontal}\:{direction}. \\ $$$$ \\ $$$$−{x}_{\mathrm{1}} {M}=\left({x}_{\mathrm{1}} +{R}\:\mathrm{sin}\:\theta\right){m} \\ $$$$\Rightarrow−{v}_{\mathrm{1}} {M}=\left({v}_{\mathrm{1}} +{R}\:\mathrm{cos}\:\theta\:\omega\right){m} \\ $$$$\Rightarrow{v}_{\mathrm{1}} =−\frac{{mR}\:\mathrm{cos}\:\theta\:\omega}{{m}+{M}}=−\frac{\mu{R}\:\mathrm{cos}\:\theta\:\omega}{\mathrm{1}+\mu} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\frac{\mu{R}}{\mathrm{1}+\mu}\left(\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} −\mathrm{cos}\:\theta\:\alpha\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{Mv}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left({v}_{\mathrm{2}{x}} ^{\mathrm{2}} +{v}_{\mathrm{2}{y}} ^{\mathrm{2}} \right)={mgR}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${v}_{\mathrm{1}} ^{\mathrm{2}} +\mu\left({v}_{\mathrm{2}{x}} ^{\mathrm{2}} +{v}_{\mathrm{2}{y}} ^{\mathrm{2}} \right)=\mathrm{2}{g}\mu{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\left(\mathrm{1}+\mu\right){v}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}\mu{R}\omega\:\mathrm{cos}\:\theta\:{v}_{\mathrm{1}} +\mu{R}^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{2}{g}\mu{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$−\frac{\mu^{\mathrm{2}} {R}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} }{\mathrm{1}+\mu}+\mu{R}^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{2}{g}\mu{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\left(\frac{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{1}+\mu}\right){R}\omega^{\mathrm{2}} =\mathrm{2}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}\left(\mathrm{1}+\mu\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{{R}\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)} \\ $$$$\Rightarrow\mathrm{2}\omega\alpha=\frac{\mathrm{2}{g}\left(\mathrm{1}+\mu\right)}{{R}}\left\{\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}−\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{2}\mu\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\right\}\omega \\ $$$$\Rightarrow\alpha=\frac{{g}\left(\mathrm{1}+\mu\right)\:\mathrm{sin}\:\theta}{{R}\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\left\{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta−\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{2}\mu\mathrm{cos}\:\theta\right\} \\ $$$$\Rightarrow\alpha=\frac{{g}\left(\mathrm{1}+\mu\right)\:\mathrm{sin}\:\theta}{{R}\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\left\{\mathrm{1}+\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right\} \\ $$$${N}=−\frac{{Ma}_{\mathrm{1}} }{\mathrm{sin}\:\theta}=−\frac{\mu{RM}}{\left(\mathrm{1}+\mu\right)\mathrm{sin}\:\theta}\left(\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} −\mathrm{cos}\:\theta\:\alpha\right) \\ $$$${N}=−\frac{\mu{RM}}{\left(\mathrm{1}+\mu\right)\mathrm{sin}\:\theta}\left\{\frac{\mathrm{2}{g}\left(\mathrm{1}+\mu\right)\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{{R}\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}−\frac{{g}\left(\mathrm{1}+\mu\right)\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\left[\mathrm{1}+\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right]}{{R}\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\right\} \\ $$$${N}=−\frac{\mu{Mg}}{\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\left\{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)−\mathrm{cos}\:\theta\:\left[\mathrm{1}+\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right]\right\} \\ $$$${N}=−\frac{\mu{Mg}}{\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\left\{\mathrm{2}−\mathrm{3cos}\:\theta+\mu\left(\mathrm{2}+\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right\} \\ $$$$\Rightarrow\frac{{N}}{{Mg}}=\frac{\mu\left[\mathrm{3cos}\:\theta−\mu\left(\mathrm{2}+\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} −\mathrm{2}\right]}{\left(\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${for}\:{N}=\mathrm{0}: \\ $$$$\mathrm{2}−\mathrm{3cos}\:\theta+\mu\left(\mathrm{2}+\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}−\mathrm{3cos}\:\theta+\mu\left(\mathrm{2}+\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{2cos}\:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mu}{\mathrm{1}+\mu}\:\mathrm{cos}^{\mathrm{3}} \:\theta−\mathrm{3}\:\mathrm{cos}\:\theta+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\lambda\:\mathrm{cos}^{\mathrm{3}} \:\alpha−\mathrm{3}\:\mathrm{cos}\:\alpha+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \left\{\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{1}−\lambda}−\mathrm{1}}{\lambda}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{1}−\lambda}+\mathrm{1}}{\lambda}}\right\} \\ $$
Commented by ajfour last updated on 19/May/19

$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{excellent}! \\ $$$$\mathrm{Your}\:\mathrm{soution}\:\mathrm{shall}\:\mathrm{determine}\:\:\mathrm{all}\: \\ $$$$\mathrm{quantities}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\theta. \\ $$
Commented by mr W last updated on 19/May/19
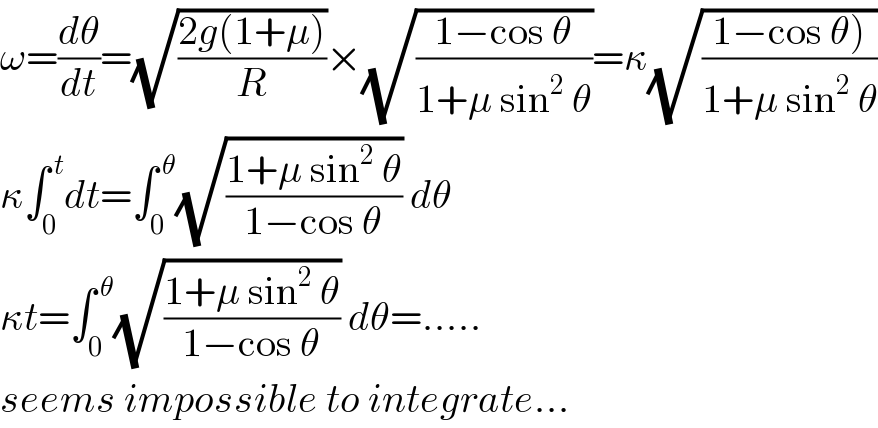
$$\omega=\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{2}{g}\left(\mathrm{1}+\mu\right)}{{R}}}×\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}}=\kappa\sqrt{\frac{\left.\mathrm{1}−\mathrm{cos}\:\theta\right)}{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\kappa\int_{\mathrm{0}} ^{\:{t}} {dt}=\int_{\mathrm{0}} ^{\:\theta} \sqrt{\frac{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{1}−\mathrm{cos}\:\theta}}\:{d}\theta \\ $$$$\kappa{t}=\int_{\mathrm{0}} ^{\:\theta} \sqrt{\frac{\mathrm{1}+\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{1}−\mathrm{cos}\:\theta}}\:{d}\theta=….. \\ $$$${seems}\:{impossible}\:{to}\:{integrate}… \\ $$
Commented by mr W last updated on 19/May/19
Commented by mr W last updated on 19/May/19
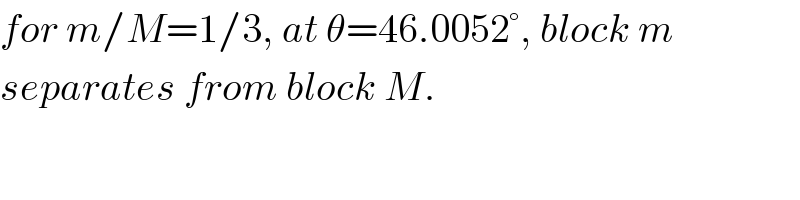
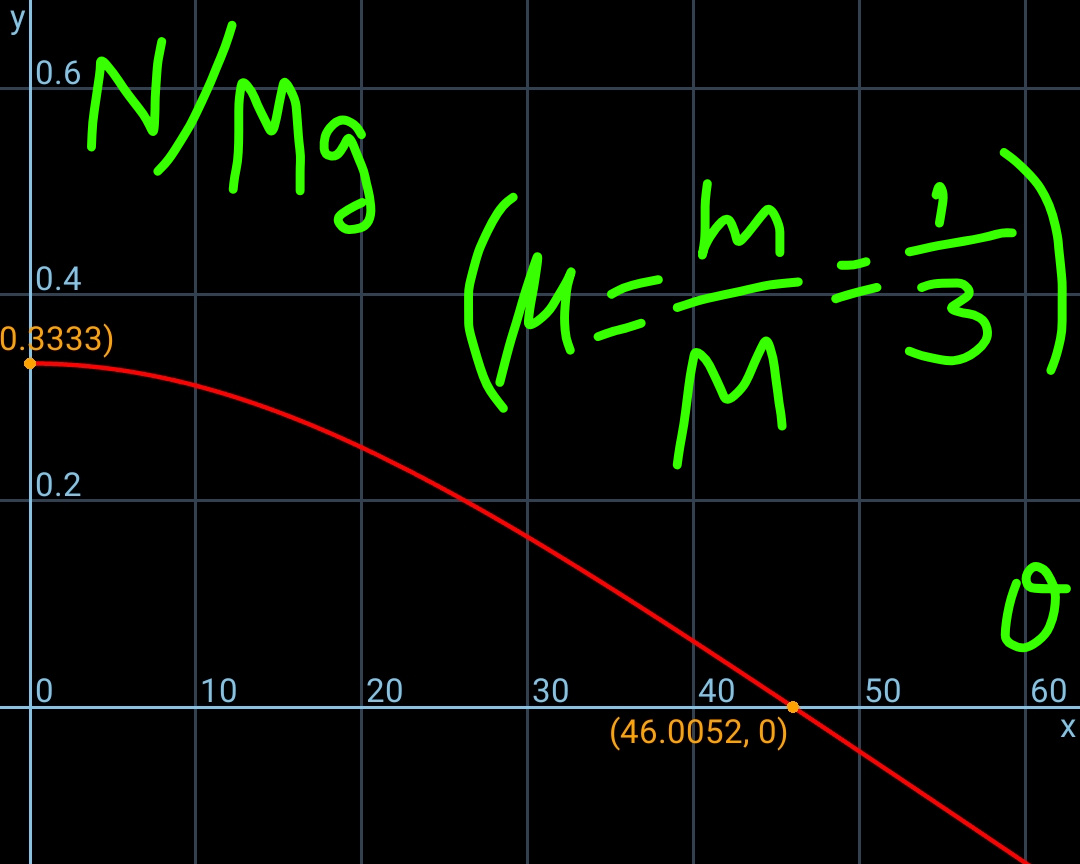
$${for}\:{m}/{M}=\mathrm{1}/\mathrm{3},\:{at}\:\theta=\mathrm{46}.\mathrm{0052}°,\:{block}\:{m} \\ $$$${separates}\:{from}\:{block}\:{M}. \\ $$
Commented by mr W last updated on 19/May/19

$${we}\:{can}\:{determine}\:{where}\:{the}\:{small}\:{block} \\ $$$${strikes}\:{the}\:{ground},\:{but}\:{we}\:{can}\:{not} \\ $$$${determine}\:{the}\:{time}\:{it}\:{takes}. \\ $$
Answered by ajfour last updated on 18/May/19
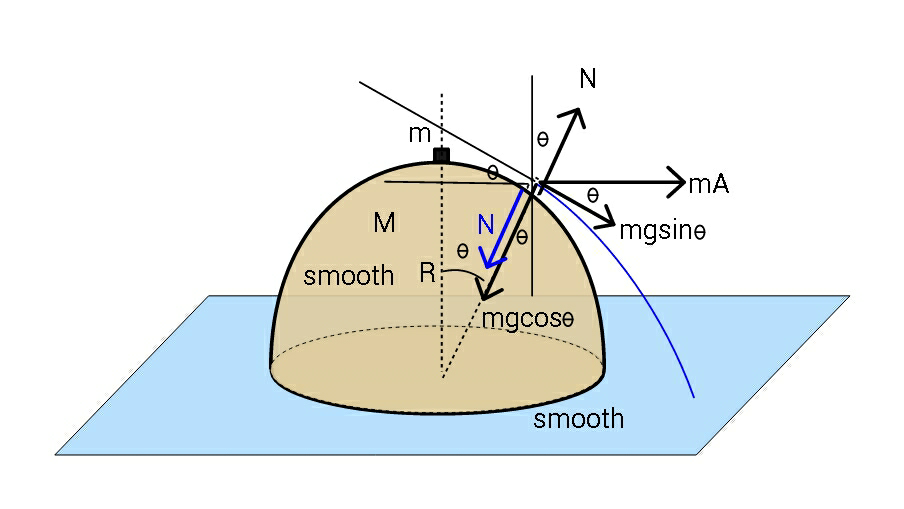
Commented by ajfour last updated on 19/May/19
![let u be velocity of block m with respect to M. Nsin θ=MA mgcos θ−N−mAsin θ=((mu^2 )/R) [when θ=α, u^2 =Rgcos α ...(I) since then N=0, A=0 ] (mgcos θ−((mu^2 )/R))sin θ=A(M+msin^2 θ) (cos θ−(u^2 /(Rg)))sin θ=(A/g)(λ+sin^2 θ) mgsin θ+mAcos θ=((mudu)/(Rdθ)) ....(II) ⇒ (1/(Rg))((udu)/dθ)=sin θ+cos θsin θ{((cos θ−(u^2 /(Rg)))/(λ+sin^2 θ))} (where λ=(M/m)) let (u^2 /(2Rg))=s (ds/dθ)=sin θ+((cos θsin θ)/(λ+sin^2 θ))(cos θ−s) ....](https://www.tinkutara.com/question/Q60180.png)
$$\mathrm{let}\:\mathrm{u}\:\mathrm{be}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{block}\:\mathrm{m} \\ $$$$\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{M}. \\ $$$$\mathrm{Nsin}\:\theta=\mathrm{MA} \\ $$$$\mathrm{mgcos}\:\theta−\mathrm{N}−\mathrm{mAsin}\:\theta=\frac{\mathrm{mu}^{\mathrm{2}} }{\mathrm{R}} \\ $$$$\:\:\:\:\:\:\left[\mathrm{when}\:\theta=\alpha,\:\:\:\mathrm{u}^{\mathrm{2}} =\mathrm{Rgcos}\:\alpha\:\:\:…\left(\mathrm{I}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\mathrm{since}\:\mathrm{then}\:\mathrm{N}=\mathrm{0},\:\mathrm{A}=\mathrm{0}\:\right] \\ $$$$\left(\mathrm{mgcos}\:\theta−\frac{\mathrm{mu}^{\mathrm{2}} }{\mathrm{R}}\right)\mathrm{sin}\:\theta=\mathrm{A}\left(\mathrm{M}+\mathrm{msin}\:^{\mathrm{2}} \theta\right) \\ $$$$\left(\mathrm{cos}\:\theta−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{Rg}}\right)\mathrm{sin}\:\theta=\frac{\mathrm{A}}{\mathrm{g}}\left(\lambda+\mathrm{sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\mathrm{mgsin}\:\theta+\mathrm{mAcos}\:\theta=\frac{\mathrm{mudu}}{\mathrm{Rd}\theta}\:\:….\left(\mathrm{II}\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{Rg}}\frac{\mathrm{udu}}{\mathrm{d}\theta}=\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\mathrm{sin}\:\theta\left\{\frac{\mathrm{cos}\:\theta−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{Rg}}}{\lambda+\mathrm{sin}\:^{\mathrm{2}} \theta}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{where}\:\:\:\:\lambda=\frac{\mathrm{M}}{\mathrm{m}}\right) \\ $$$$\:\:\:\mathrm{let}\:\:\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2Rg}}=\mathrm{s} \\ $$$$\:\:\:\frac{\mathrm{ds}}{\mathrm{d}\theta}=\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta\mathrm{sin}\:\theta}{\lambda+\mathrm{sin}\:^{\mathrm{2}} \theta}\left(\mathrm{cos}\:\theta−\mathrm{s}\right) \\ $$$$…. \\ $$
Commented by ajfour last updated on 19/May/19
![mgR(1−cos α)=(1/2)MV^2 +(1/2)m[(ucos α−V)^2 +u^2 sin^2 α] (energy conservation) mucos α = (M+m)V (momentum conservation along horizontal) u^2 =Rgcos α ⇒ 2mgR(1−cos α)=M((m/(M+m)))^2 (Rgcos α)cos^2 α +m[Rgcos^3 α(1−(m/(M+m)))^2 +Rgcos αsin^2 α] ⇒ 2(1−cos α)=((λcos^3 α)/((λ+1)^2 ))+((λ/(λ+1)))^2 cos^3 α +cos αsin^2 α let cos α=x 3x−(1/(λ+1))x^3 −2=0 say if λ>>1 ⇒ x=cos α = (2/3) , α=cos^(−1) (2/3) ≈48.19° if M=3m ⇒ λ=3 3x−(x^3 /4)−2=0 or cos^3 α−12cos α+8 =0 ⇒ α≈ 46.005° .](https://www.tinkutara.com/question/Q60183.png)
$$\mathrm{mgR}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}\left[\left(\mathrm{ucos}\:\alpha−\mathrm{V}\right)^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{energy}\:\mathrm{conservation}\right) \\ $$$$\mathrm{mucos}\:\alpha\:=\:\left(\mathrm{M}+\mathrm{m}\right)\mathrm{V}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{momentum}\:\mathrm{conservation}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{along}\:\mathrm{horizontal}\right) \\ $$$$\mathrm{u}^{\mathrm{2}} =\mathrm{Rgcos}\:\alpha \\ $$$$\Rightarrow\:\mathrm{2mgR}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)=\mathrm{M}\left(\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)^{\mathrm{2}} \left(\mathrm{Rgcos}\:\alpha\right)\mathrm{cos}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{m}\left[\mathrm{Rgcos}\:^{\mathrm{3}} \alpha\left(\mathrm{1}−\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)^{\mathrm{2}} +\mathrm{Rgcos}\:\alpha\mathrm{sin}\:^{\mathrm{2}} \alpha\right] \\ $$$$\Rightarrow \\ $$$$\:\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)=\frac{\lambda\mathrm{cos}\:^{\mathrm{3}} \alpha}{\left(\lambda+\mathrm{1}\right)^{\mathrm{2}} }+\left(\frac{\lambda}{\lambda+\mathrm{1}}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{3}} \alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{cos}\:\alpha\mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\mathrm{let}\:\:\mathrm{cos}\:\alpha=\mathrm{x} \\ $$$$\:\:\mathrm{3x}−\frac{\mathrm{1}}{\lambda+\mathrm{1}}\mathrm{x}^{\mathrm{3}} −\mathrm{2}=\mathrm{0} \\ $$$$\:\mathrm{say}\:\mathrm{if}\:\lambda>>\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}=\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:,\:\:\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\:\approx\mathrm{48}.\mathrm{19}° \\ $$$$\mathrm{if}\:\:\mathrm{M}=\mathrm{3m}\:\:\Rightarrow\:\lambda=\mathrm{3} \\ $$$$\:\:\mathrm{3x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{4}}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{or}\:\:\:\:\:\mathrm{cos}\:^{\mathrm{3}} \alpha−\mathrm{12cos}\:\alpha+\mathrm{8}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:\:\:\:\alpha\approx\:\mathrm{46}.\mathrm{005}°\:. \\ $$
Commented by mr W last updated on 19/May/19
$${your}\:{method}\:{is}\:{absolutely}\:{correct}\:{sir}! \\ $$
Commented by ajfour last updated on 19/May/19

$${thank}\:{you}\:{Sir}! \\ $$
Commented by mr W last updated on 19/May/19

$${you}\:{use}\:{directly}\:{the}\:{motion}\:{eqn}.\:{in} \\ $$$${radial}\:{and}\:{tangential}\:{directions},\: \\ $$$${while}\:{i}\:{usually}\:{derive}\:{the}\:{velocity} \\ $$$${and}\:{acceleration}\:{from}\:{the}\:{x}−\:{and} \\ $$$${y}−{coordinates}\:{which}\:{is}\:{mostly} \\ $$$${lengthy}\:{and}\:{complicated}.\:{your} \\ $$$${method}\:{is}\:{thus}\:{shorter}\:{and}\:{better}. \\ $$
