Question Number 60283 by mr W last updated on 19/May/19
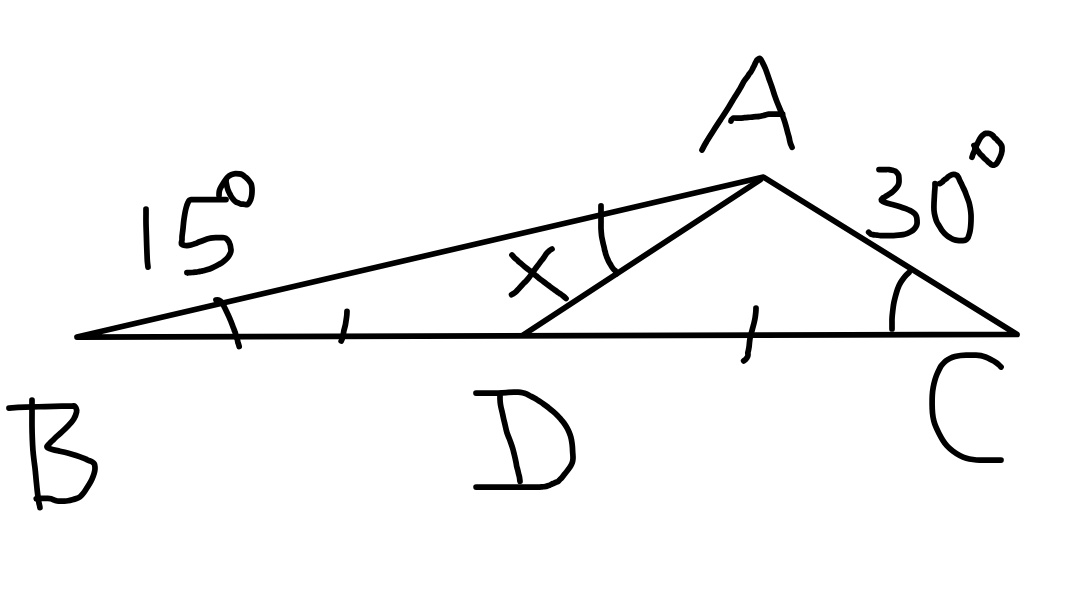
Commented by mr W last updated on 19/May/19
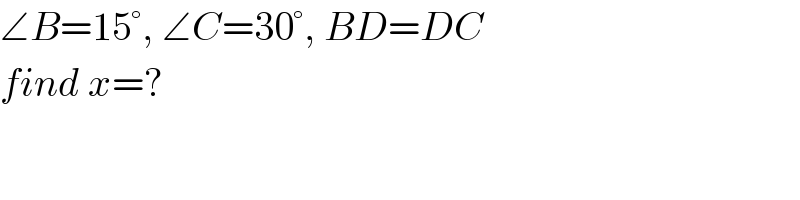
$$\angle{B}=\mathrm{15}°,\:\angle{C}=\mathrm{30}°,\:{BD}={DC} \\ $$$${find}\:{x}=? \\ $$
Answered by ajfour last updated on 19/May/19
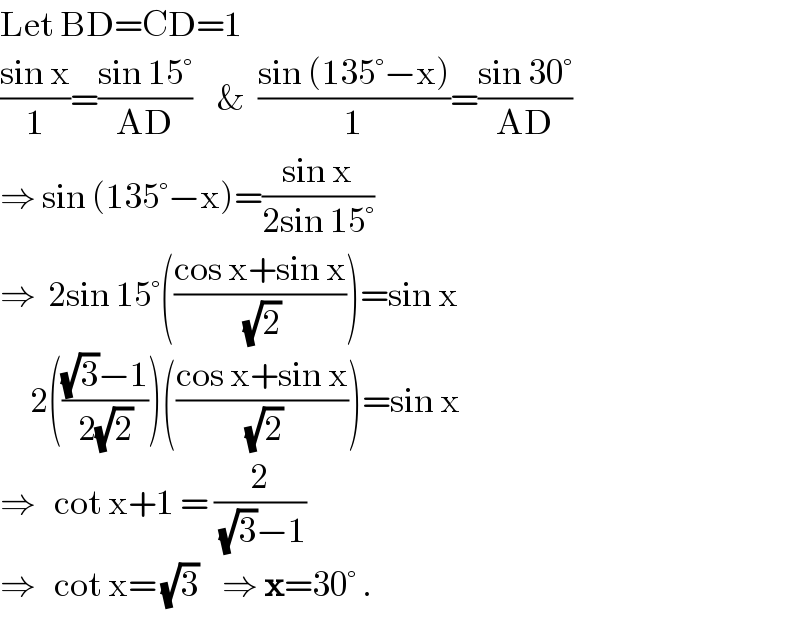
$$\mathrm{Let}\:\mathrm{BD}=\mathrm{CD}=\mathrm{1} \\ $$$$\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}}=\frac{\mathrm{sin}\:\mathrm{15}°}{\mathrm{AD}}\:\:\:\:\&\:\:\frac{\mathrm{sin}\:\left(\mathrm{135}°−\mathrm{x}\right)}{\mathrm{1}}=\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{AD}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\mathrm{135}°−\mathrm{x}\right)=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2sin}\:\mathrm{15}°} \\ $$$$\Rightarrow\:\:\mathrm{2sin}\:\mathrm{15}°\left(\frac{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\left(\frac{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{sin}\:\mathrm{x} \\ $$$$\Rightarrow\:\:\:\mathrm{cot}\:\mathrm{x}+\mathrm{1}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}−\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\mathrm{cot}\:\mathrm{x}=\:\sqrt{\mathrm{3}}\:\:\:\:\Rightarrow\:\boldsymbol{\mathrm{x}}=\mathrm{30}°\:. \\ $$
Commented by mr W last updated on 19/May/19

$${thanks}\:{alot}\:{sir}! \\ $$
