Menu Close

Question-60313

Tinku Tara 0 Comments
Pin




Question Number 60313 by ajfour last updated on 19/May/19
Commented by ajfour last updated on 19/May/19
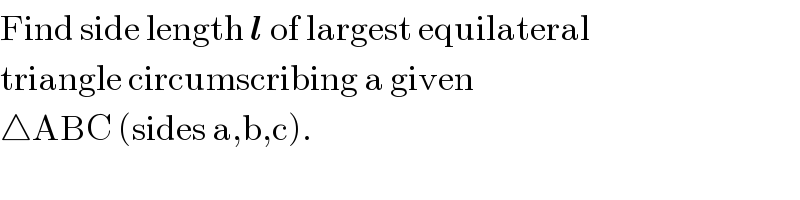
Find side length l of largest equilateral triangle circumscribing a given △ABC (sides a,b,c).
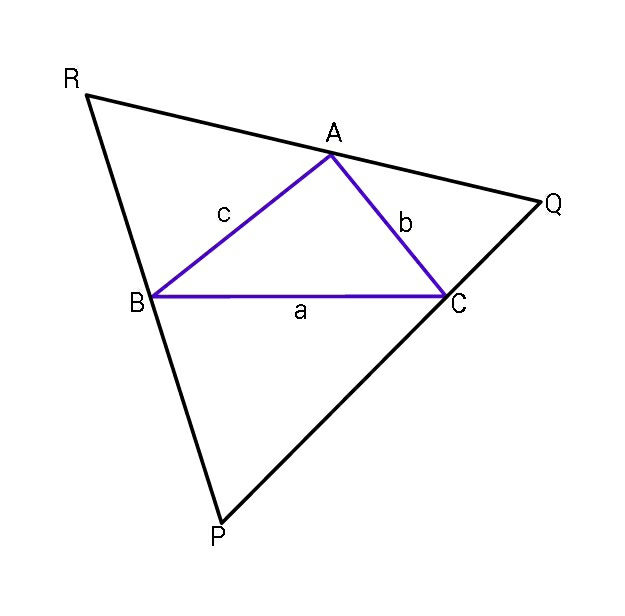
$$\mathrm{Find}\:\mathrm{side}\:\mathrm{length}\:\boldsymbol{{l}}\:\mathrm{of}\:\mathrm{largest}\:\mathrm{equilateral} \\ $$$$\mathrm{triangle}\:\mathrm{circumscribing}\:\mathrm{a}\:\mathrm{given} \\ $$$$\bigtriangleup\mathrm{ABC}\:\left(\mathrm{sides}\:\mathrm{a},\mathrm{b},\mathrm{c}\right). \\ $$
Answered by ajfour last updated on 19/May/19
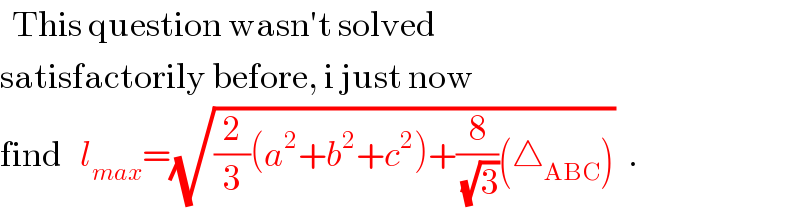
This question wasn′t solved satisfactorily before, i just now find l_(max) =(√((2/3)(a^2 +b^2 +c^2 )+(8/( (√3)))(△_(ABC) ))) .
$$\:\:\mathrm{This}\:\mathrm{question}\:\mathrm{wasn}'\mathrm{t}\:\mathrm{solved} \\ $$$$\mathrm{satisfactorily}\:\mathrm{before},\:\mathrm{i}\:\mathrm{just}\:\mathrm{now} \\ $$$$\mathrm{find}\:\:\:{l}_{{max}} =\sqrt{\frac{\mathrm{2}}{\mathrm{3}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\left(\bigtriangleup_{\mathrm{ABC}} \right)}\:\:. \\ $$
Commented by ajfour last updated on 21/May/19
dont you like this solution mrW Sir, it is to meet your previous objection to a previous coordinate geometry based solution of mine which wasn′t as symmetric in a,b,c as this; if you remember it at all..
$$\mathrm{dont}\:\mathrm{you}\:\mathrm{like}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{mrW}\:\mathrm{Sir}, \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{to}\:\mathrm{meet}\:\mathrm{your}\:\mathrm{previous}\:\mathrm{objection} \\ $$$$\mathrm{to}\:\mathrm{a}\:\mathrm{previous}\:\mathrm{coordinate}\:\mathrm{geometry} \\ $$$$\mathrm{based}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{mine}\:\mathrm{which}\:\mathrm{wasn}'\mathrm{t} \\ $$$$\mathrm{as}\:\mathrm{symmetric}\:\mathrm{in}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{as}\:\mathrm{this};\:\mathrm{if}\:\mathrm{you} \\ $$$$\mathrm{remember}\:\mathrm{it}\:\mathrm{at}\:\mathrm{all}.. \\ $$
Commented by mr W last updated on 22/May/19
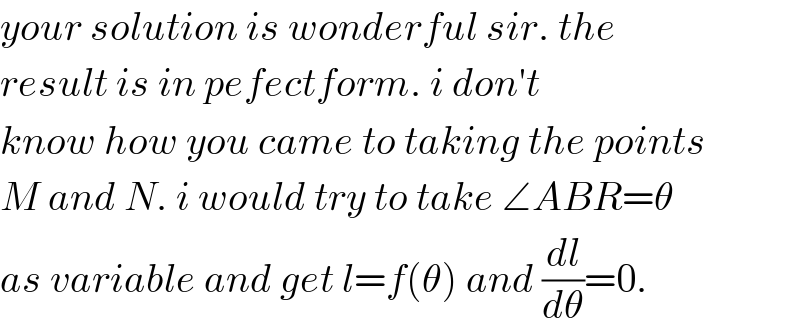
your solution is wonderful sir. the result is in pefectform. i don′t know how you came to taking the points M and N. i would try to take ∠ABR=θ as variable and get l=f(θ) and (dl/dθ)=0.
$${your}\:{solution}\:{is}\:{wonderful}\:{sir}.\:{the} \\ $$$${result}\:{is}\:{in}\:{pefectform}.\:{i}\:{don}'{t} \\ $$$${know}\:{how}\:{you}\:{came}\:{to}\:{taking}\:{the}\:{points} \\ $$$${M}\:{and}\:{N}.\:{i}\:{would}\:{try}\:{to}\:{take}\:\angle{ABR}=\theta \\ $$$${as}\:{variable}\:{and}\:{get}\:{l}={f}\left(\theta\right)\:{and}\:\frac{{dl}}{{d}\theta}=\mathrm{0}. \\ $$
Commented by ajfour last updated on 21/May/19
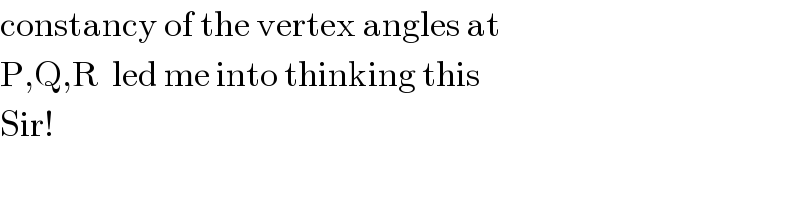
constancy of the vertex angles at P,Q,R led me into thinking this Sir!
$$\mathrm{constancy}\:\mathrm{of}\:\mathrm{the}\:\mathrm{vertex}\:\mathrm{angles}\:\mathrm{at} \\ $$$$\mathrm{P},\mathrm{Q},\mathrm{R}\:\:\mathrm{led}\:\mathrm{me}\:\mathrm{into}\:\mathrm{thinking}\:\mathrm{this}\: \\ $$$$\mathrm{Sir}! \\ $$
Commented by mr W last updated on 21/May/19
great thought sir! this gives the answer to my question how to determine the max. circumscribing equilateral triangle geometrically, i.e. without using calculus. i have been thinking about this for two days. now i know how. it answers also the question that the searched triangle is a maximum, not a minimum.
$${great}\:{thought}\:{sir}!\:{this}\:{gives}\:{the} \\ $$$${answer}\:{to}\:{my}\:{question}\:{how}\:{to}\:{determine} \\ $$$${the}\:{max}.\:{circumscribing}\:{equilateral} \\ $$$${triangle}\:{geometrically}, \\ $$$${i}.{e}.\:{without}\:{using}\:{calculus}. \\ $$$${i}\:{have}\:{been}\:{thinking}\:{about} \\ $$$${this}\:{for}\:{two}\:{days}.\:{now}\:{i}\:{know}\:{how}. \\ $$$${it}\:{answers}\:{also}\:{the}\:{question}\:{that} \\ $$$${the}\:{searched}\:{triangle}\:{is}\:{a}\:{maximum}, \\ $$$${not}\:{a}\:{minimum}. \\ $$
Commented by mr W last updated on 21/May/19
my result using geometrical method is the same as your method using calculus, see below.
$${my}\:{result}\:{using}\:{geometrical}\:{method} \\ $$$${is}\:{the}\:{same}\:{as}\:{your}\:{method}\:{using} \\ $$$${calculus},\:{see}\:{below}. \\ $$
Answered by ajfour last updated on 20/May/19
Commented by ajfour last updated on 20/May/19
cos 30° = ((BC/2)/(CM)) ⇒ ((√3)/2)=(a/2)×(1/(CM)) ⇒ PM=CM=(a/( (√3))) (similarly BN=(c/( (√3))) ) .....(ii) ∠BMP=180°−60°−θ BP=2PMsin (((∠BMP)/2)) BP=((2a)/( (√3)))sin (60°−(θ/2)) ......(i) let ∠B=β and since ∠PBR=180°, φ+30°+β+30°+(30°+(θ/2))=180° ⇒ φ=90°−β−(θ/2) BR = 2BNcos φ =((2c)/( (√3)))sin (β+(θ/2)) let side of equilateral △PQR be l. l= BP+BR = ((2a)/( (√3)))sin (60°−(θ/2))+((2c)/( (√3)))sin (β+(θ/2)) ⇒l(√(3 ))=a((√3)cos (θ/2)−sin (θ/2)) +2c(sin βcos (θ/2)+cos βsin (θ/2)) l(√3) =(2ccos β−a)sin (θ/2) +(2csin β+a(√3))cos (θ/2) ((d(l(√3)))/dθ)=0 ⇒ tan (θ/2)=((2ccos β−a)/(2csin β+a(√3))) l(√3)= (2ccos β−a){sin (θ/2)+((cos^2 (θ/2))/(sin (θ/2)))} l(√3) = ((2ccos β−a)/(sin (θ/2))) l_(max) (√3) = (√((2ccos β−a)^2 +(2csin β+a(√3))^2 )) =(√(4a^2 +4c^2 +4ac((√3)sin β−cos β))) = (√(4a^2 +4c^2 +8(√3)((1/2)acsin β)−4ac(((a^2 +c^2 −b^2 )/(2ac))))) ⇒l(√3) = (√(2(a^2 +b^2 +c^2 )+8(√3)△_(ABC) )) ___________________________ l_(max) =(√((2/3)(a^2 +b^2 +c^2 )+(8/( (√3)))△_(ABC) )) ___________________________.
$$\mathrm{cos}\:\mathrm{30}°\:=\:\frac{\mathrm{BC}/\mathrm{2}}{\mathrm{CM}}\:\:\:\Rightarrow\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{a}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{CM}} \\ $$$$\Rightarrow\:\:\:\mathrm{PM}=\mathrm{CM}=\frac{\mathrm{a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\left(\mathrm{similarly}\:\:\mathrm{BN}=\frac{\mathrm{c}}{\:\sqrt{\mathrm{3}}}\:\:\right)\:\:\:…..\left(\mathrm{ii}\right) \\ $$$$\angle\mathrm{BMP}=\mathrm{180}°−\mathrm{60}°−\theta \\ $$$$\mathrm{BP}=\mathrm{2PMsin}\:\left(\frac{\angle\mathrm{BMP}}{\mathrm{2}}\right) \\ $$$$\mathrm{BP}=\frac{\mathrm{2a}}{\:\sqrt{\mathrm{3}}}\mathrm{sin}\:\left(\mathrm{60}°−\frac{\theta}{\mathrm{2}}\right)\:\:\:\:\:\:\:\:……\left(\mathrm{i}\right) \\ $$$$\mathrm{let}\:\angle\mathrm{B}=\beta\:\:\mathrm{and}\:\mathrm{since}\:\angle\mathrm{PBR}=\mathrm{180}°, \\ $$$$\phi+\mathrm{30}°+\beta+\mathrm{30}°+\left(\mathrm{30}°+\frac{\theta}{\mathrm{2}}\right)=\mathrm{180}° \\ $$$$\Rightarrow\:\:\:\phi=\mathrm{90}°−\beta−\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\mathrm{BR}\:=\:\mathrm{2BNcos}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2c}}{\:\sqrt{\mathrm{3}}}\mathrm{sin}\:\left(\beta+\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{let}\:\mathrm{side}\:\mathrm{of}\:\mathrm{equilateral}\:\bigtriangleup\mathrm{PQR}\:\mathrm{be}\:\boldsymbol{{l}}. \\ $$$$\:{l}=\:\mathrm{BP}+\mathrm{BR} \\ $$$$\:\:\:\:=\:\frac{\mathrm{2a}}{\:\sqrt{\mathrm{3}}}\mathrm{sin}\:\left(\mathrm{60}°−\frac{\theta}{\mathrm{2}}\right)+\frac{\mathrm{2c}}{\:\sqrt{\mathrm{3}}}\mathrm{sin}\:\left(\beta+\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow{l}\sqrt{\mathrm{3}\:}={a}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2c}\left(\mathrm{sin}\:\beta\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{cos}\:\beta\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\:\:\:\:{l}\sqrt{\mathrm{3}}\:=\left(\mathrm{2ccos}\:\beta−\mathrm{a}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{2csin}\:\beta+\mathrm{a}\sqrt{\mathrm{3}}\right)\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\frac{{d}\left({l}\sqrt{\mathrm{3}}\right)}{{d}\theta}=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\:\:\:\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{2ccos}\:\beta−\mathrm{a}}{\mathrm{2csin}\:\beta+\mathrm{a}\sqrt{\mathrm{3}}} \\ $$$$\:\:{l}\sqrt{\mathrm{3}}=\:\left(\mathrm{2}{c}\mathrm{cos}\:\beta−\mathrm{a}\right)\left\{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}+\frac{\mathrm{cos}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\right\} \\ $$$$\:\:\:\:\:\:\:{l}\sqrt{\mathrm{3}}\:\:=\:\:\frac{\mathrm{2ccos}\:\beta−\mathrm{a}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\:{l}_{{max}} \sqrt{\mathrm{3}}\:=\:\sqrt{\left(\mathrm{2}{c}\mathrm{cos}\:\beta−\mathrm{a}\right)^{\mathrm{2}} +\left(\mathrm{2csin}\:\beta+\mathrm{a}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\sqrt{\mathrm{4a}^{\mathrm{2}} +\mathrm{4c}^{\mathrm{2}} +\mathrm{4ac}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\beta−\mathrm{cos}\:\beta\right)} \\ $$$$\:\:\:\:\:=\:\sqrt{\mathrm{4a}^{\mathrm{2}} +\mathrm{4c}^{\mathrm{2}} +\mathrm{8}\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{acsin}\:\beta\right)−\mathrm{4ac}\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}}\right)} \\ $$$$\:\:\Rightarrow\boldsymbol{{l}}\sqrt{\mathrm{3}}\:=\:\sqrt{\mathrm{2}\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \right)+\mathrm{8}\sqrt{\mathrm{3}}\bigtriangleup_{\mathrm{ABC}} } \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\boldsymbol{{l}}_{\boldsymbol{{max}}} =\sqrt{\frac{\mathrm{2}}{\mathrm{3}}\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \right)+\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\bigtriangleup_{\mathrm{ABC}} } \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$$$ \\ $$
Commented by ajfour last updated on 20/May/19
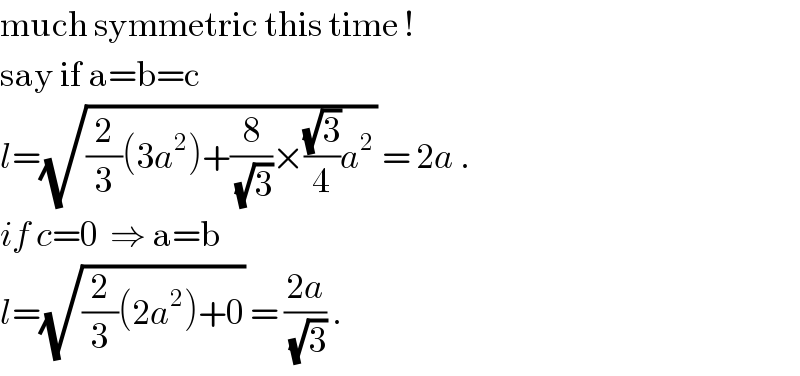
much symmetric this time ! say if a=b=c l=(√((2/3)(3a^2 )+(8/( (√3)))×((√3)/4)a^2 )) = 2a . if c=0 ⇒ a=b l=(√((2/3)(2a^2 )+0)) = ((2a)/( (√3))) .
$$\mathrm{much}\:\mathrm{symmetric}\:\mathrm{this}\:\mathrm{time}\:!\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{say}\:\mathrm{if}\:\mathrm{a}=\mathrm{b}=\mathrm{c} \\ $$$${l}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{3}{a}^{\mathrm{2}} \right)+\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}^{\mathrm{2}} }\:=\:\mathrm{2}{a}\:. \\ $$$${if}\:{c}=\mathrm{0}\:\:\Rightarrow\:\mathrm{a}=\mathrm{b} \\ $$$${l}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{a}^{\mathrm{2}} \right)+\mathrm{0}}\:=\:\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}}\:. \\ $$
Answered by mr W last updated on 21/May/19
Commented by mr W last updated on 03/Feb/24
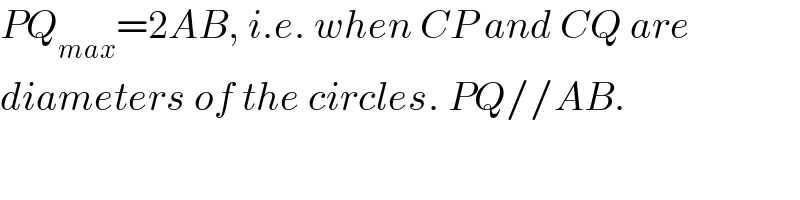
PQ_(max) =2AB, i.e. when CP and CQ are diameters of the circles. PQ//AB.
$${PQ}_{{max}} =\mathrm{2}{AB},\:{i}.{e}.\:{when}\:{CP}\:{and}\:{CQ}\:{are} \\ $$$${diameters}\:{of}\:{the}\:{circles}.\:{PQ}//{AB}. \\ $$
Commented by mr W last updated on 21/May/19
this is the geometrical solution: construct point M and point N such that ∠BMC=120° and ∠ANB=120°. construct circle with point M as center and through B and C. construct circle with point N as center and through A and B. both circles intersect at point D. construct diameter DP and DR. PR is the side length of the maximum equilateral triangle PQR which we are searching.
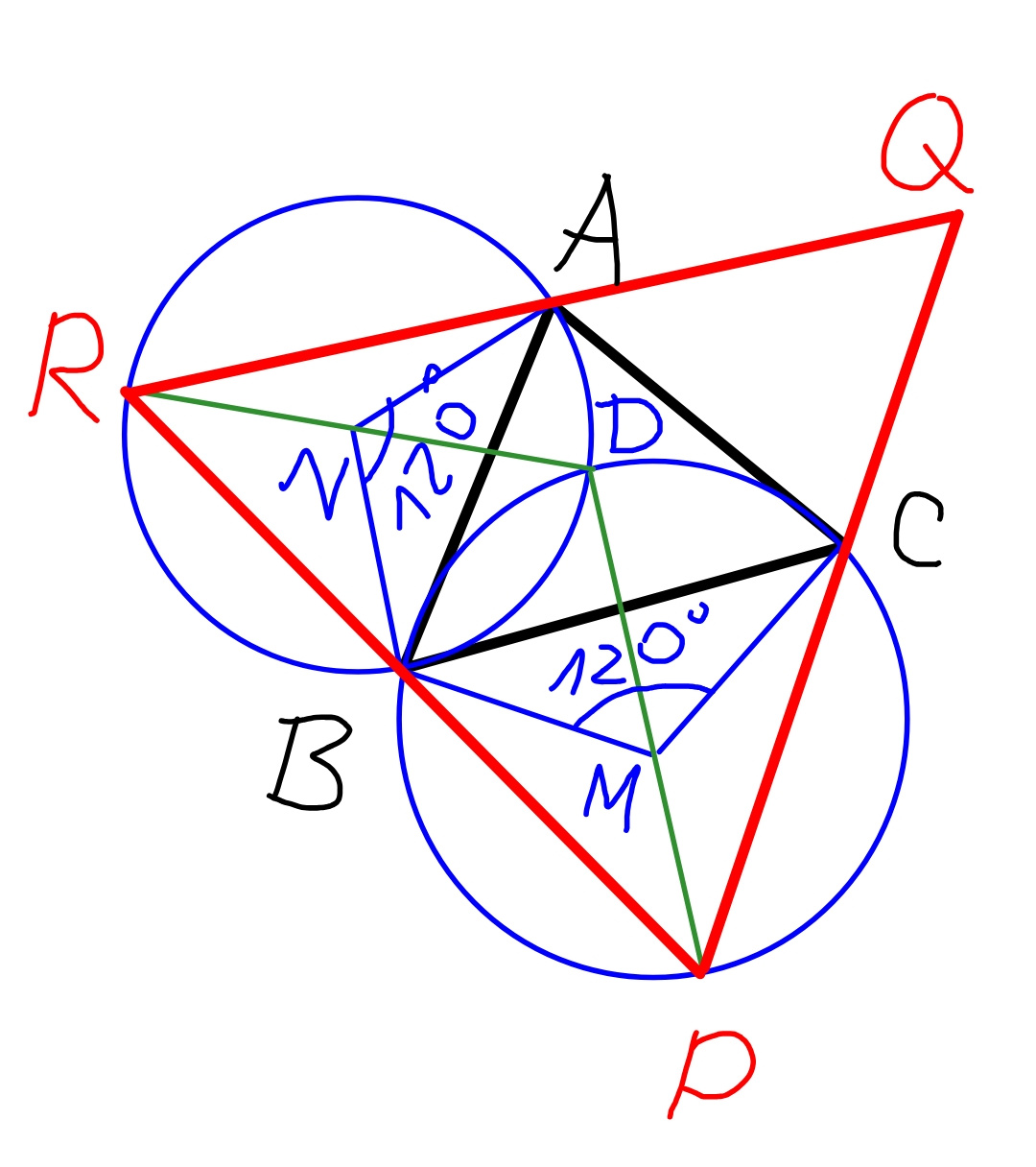
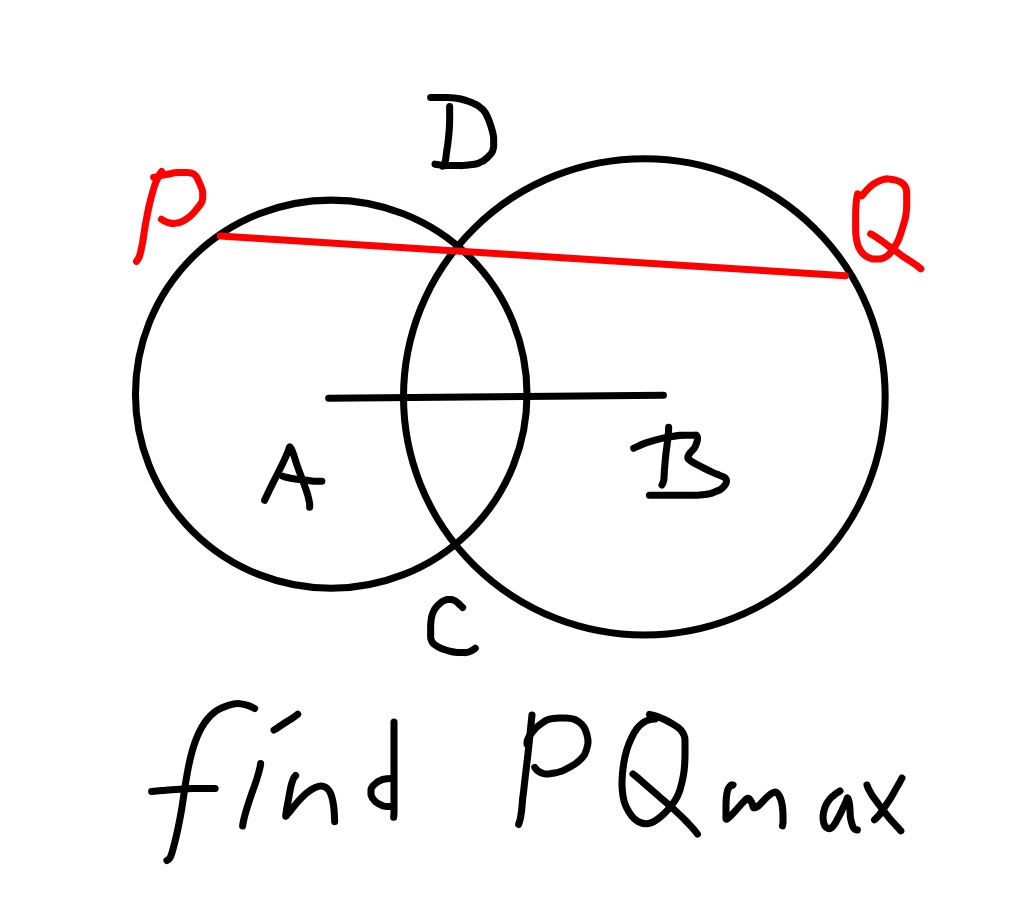
$${this}\:{is}\:{the}\:{geometrical}\:{solution}: \\ $$$${construct}\:{point}\:{M}\:{and}\:{point}\:{N}\:{such} \\ $$$${that}\:\angle{BMC}=\mathrm{120}°\:{and}\:\angle{ANB}=\mathrm{120}°. \\ $$$${construct}\:{circle}\:{with}\:{point}\:{M}\:{as} \\ $$$${center}\:{and}\:{through}\:{B}\:{and}\:{C}. \\ $$$${construct}\:{circle}\:{with}\:{point}\:{N}\:{as} \\ $$$${center}\:{and}\:{through}\:{A}\:{and}\:{B}. \\ $$$${both}\:{circles}\:{intersect}\:{at}\:{point}\:{D}. \\ $$$${construct}\:{diameter}\:{DP}\:{and}\:{DR}. \\ $$$${PR}\:{is}\:{the}\:{side}\:{length}\:{of}\:{the}\:{maximum} \\ $$$${equilateral}\:{triangle}\:{PQR}\:{which}\:{we} \\ $$$${are}\:{searching}. \\ $$
Commented by mr W last updated on 21/May/19
MB=MC=(a/2)×(2/( (√3)))=(a/( (√3))) NB=NA=(c/2)×(2/( (√3)))=(c/( (√3))) ∠MBN=∠B+60° MN^2 =BN^2 +BM^2 −2×BM×BN×cos (B+60°) =(a^2 /3)+(c^2 /3)−((2ac )/3)((1/2)cos B−((√3)/2) sin B) =((a^2 +c^2 )/3)−((ac cos B )/3)+(1/( (√3))) ac sin B =((a^2 +c^2 )/3)−((ac(a^2 +c^2 −b^2 ) )/(6ac))+(1/( (√3))) ac sin B =((a^2 +b^2 +c^2 )/6)+(1/( (√3))) ac sin B l=PR=2MN=2(√(((a^2 +b^2 +c^2 )/6)+(1/( (√3))) ac sin B)) =(√(((2(a^2 +b^2 +c^2 ) )/3)+((4 ac sin B)/( (√3))))) since Δ=((ac sin B)/2)=area of ΔABC ⇒l=(√(((2(a^2 +b^2 +c^2 ) )/3)+((8Δ)/( (√3)))))
$${MB}={MC}=\frac{{a}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$$${NB}={NA}=\frac{{c}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}=\frac{{c}}{\:\sqrt{\mathrm{3}}} \\ $$$$\angle{MBN}=\angle{B}+\mathrm{60}° \\ $$$${MN}^{\mathrm{2}} ={BN}^{\mathrm{2}} +{BM}^{\mathrm{2}} −\mathrm{2}×{BM}×{BN}×\mathrm{cos}\:\left({B}+\mathrm{60}°\right) \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{3}}+\frac{{c}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{2}{ac}\:}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{B}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{sin}\:{B}\right) \\ $$$$=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}−\frac{{ac}\:\mathrm{cos}\:{B}\:}{\mathrm{3}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{ac}\:\mathrm{sin}\:{B} \\ $$$$=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}−\frac{{ac}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:}{\mathrm{6}{ac}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{ac}\:\mathrm{sin}\:{B} \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \:}{\mathrm{6}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{ac}\:\mathrm{sin}\:{B} \\ $$$${l}={PR}=\mathrm{2}{MN}=\mathrm{2}\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \:}{\mathrm{6}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{ac}\:\mathrm{sin}\:{B}} \\ $$$$=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:}{\mathrm{3}}+\frac{\mathrm{4}\:{ac}\:\mathrm{sin}\:{B}}{\:\sqrt{\mathrm{3}}}} \\ $$$${since}\:\Delta=\frac{{ac}\:\mathrm{sin}\:{B}}{\mathrm{2}}={area}\:{of}\:\Delta{ABC} \\ $$$$\Rightarrow{l}=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:}{\mathrm{3}}+\frac{\mathrm{8}\Delta}{\:\sqrt{\mathrm{3}}}} \\ $$
Commented by ajfour last updated on 22/May/19
Why this way we get the maximum size △PQR , i fail to follow the reason, Sir; please enlighten..
$$\mathrm{Why}\:\mathrm{this}\:\mathrm{way}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{size}\:\bigtriangleup\mathrm{PQR}\:,\:\mathrm{i}\:\mathrm{fail}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{reason}, \\ $$$$\mathrm{Sir};\:\mathrm{please}\:\mathrm{enlighten}.. \\ $$
Commented by mr W last updated on 22/May/19
we can see that R must be on the circle with center N and P on the circle with center M. now the question is to find the positions of P and R such that PR reaches the maximum. we can see ∠DPB and ∠DRB are both constant, therefore ∠PDR is also constant. in this case the PR reaches its msximum if both DP and DR reach their maximum, i.e. when DP and DR are the diameters of the circles. i can remember once i put this question in an earlier post, and you have solved it using calculus method. unfortunately i can not find this old post, but maybe you can also remember it, see image below.
$${we}\:{can}\:{see}\:{that}\:{R}\:{must}\:{be}\:{on}\:{the}\:{circle} \\ $$$${with}\:{center}\:{N}\:{and}\:{P}\:{on}\:{the}\:{circle}\:{with} \\ $$$${center}\:{M}.\:\:{now}\:{the}\:{question}\:{is}\:{to}\:{find} \\ $$$${the}\:{positions}\:{of}\:{P}\:{and}\:{R}\:{such}\:{that}\:{PR} \\ $$$${reaches}\:{the}\:{maximum}. \\ $$$${we}\:{can}\:{see}\:\angle{DPB}\:{and}\:\angle{DRB}\:{are}\:{both} \\ $$$${constant},\:{therefore}\:\angle{PDR}\:{is}\:{also}\: \\ $$$${constant}.\:{in}\:{this}\:{case}\:{the}\:{PR}\:{reaches} \\ $$$${its}\:{msximum}\:{if}\:{both}\:{DP}\:{and}\:{DR} \\ $$$${reach}\:{their}\:{maximum},\:{i}.{e}.\:{when} \\ $$$${DP}\:{and}\:{DR}\:{are}\:{the}\:{diameters}\:{of}\:{the} \\ $$$${circles}.\:{i}\:{can}\:{remember}\:{once}\:{i}\:{put} \\ $$$${this}\:{question}\:{in}\:{an}\:{earlier}\:{post},\:{and} \\ $$$${you}\:{have}\:{solved}\:{it}\:{using}\:{calculus} \\ $$$${method}.\:{unfortunately}\:{i}\:{can}\:{not} \\ $$$${find}\:{this}\:{old}\:{post},\:{but}\:{maybe}\:{you}\:{can} \\ $$$${also}\:{remember}\:{it},\:{see}\:{image}\:{below}. \\ $$
Commented by mr W last updated on 22/May/19
Commented by ajfour last updated on 22/May/19
Thanks Sir, for the geometric way!
$$\mathrm{Thanks}\:\mathrm{Sir},\:\mathrm{for}\:\mathrm{the}\:\mathrm{geometric}\:\mathrm{way}! \\ $$
Commented by mr W last updated on 22/May/19
this is a very interesting question. i spent a long time to find a way to understand and solve it geometrically. i′d never come to this solution without your image. therefore thanks alot!
$${this}\:{is}\:{a}\:{very}\:{interesting}\:{question}. \\ $$$${i}\:{spent}\:{a}\:{long}\:{time}\:{to}\:{find}\:{a}\:{way}\:{to} \\ $$$${understand}\:{and}\:{solve}\:{it}\:{geometrically}. \\ $$$${i}'{d}\:{never}\:{come}\:{to}\:{this}\:{solution}\:{without} \\ $$$${your}\:{image}.\:{therefore}\:{thanks}\:{alot}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *