Menu Close

Question-60318

Tinku Tara 0 Comments
Pin




Question Number 60318 by Sardor2211 last updated on 19/May/19
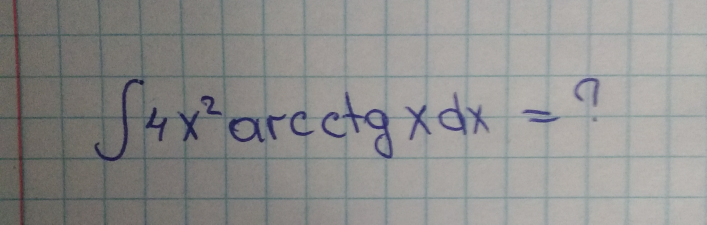
Commented by kaivan.ahmadi last updated on 20/May/19
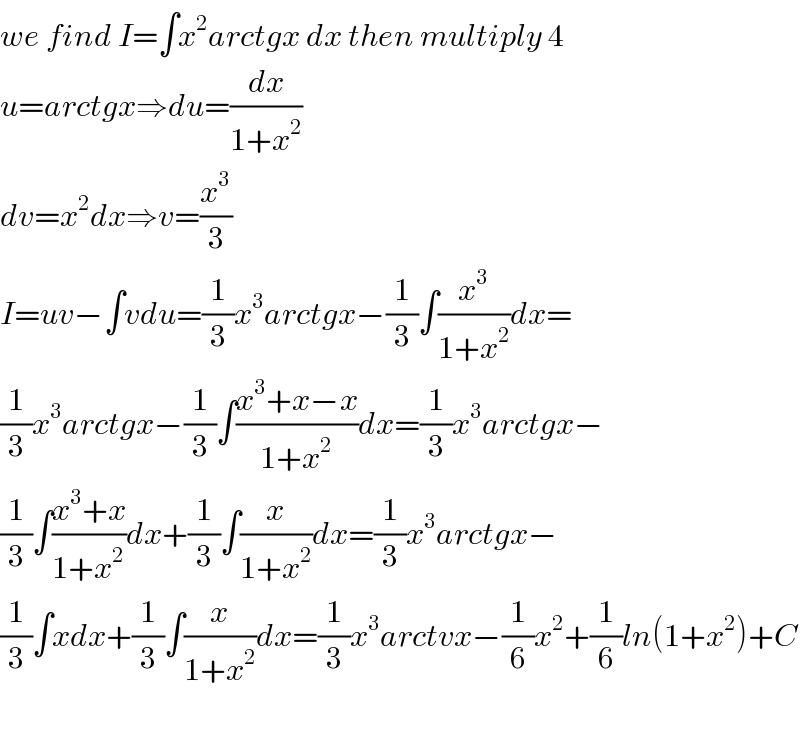
we find I=∫x^2 arctgx dx then multiply 4 u=arctgx⇒du=(dx/(1+x^2 )) dv=x^2 dx⇒v=(x^3 /3) I=uv−∫vdu=(1/3)x^3 arctgx−(1/3)∫(x^3 /(1+x^2 ))dx= (1/3)x^3 arctgx−(1/3)∫((x^3 +x−x)/(1+x^2 ))dx=(1/3)x^3 arctgx− (1/3)∫((x^3 +x)/(1+x^2 ))dx+(1/3)∫(x/(1+x^2 ))dx=(1/3)x^3 arctgx− (1/3)∫xdx+(1/3)∫(x/(1+x^2 ))dx=(1/3)x^3 arctvx−(1/6)x^2 +(1/6)ln(1+x^2 )+C
$${we}\:{find}\:{I}=\int{x}^{\mathrm{2}} {arctgx}\:{dx}\:{then}\:{multiply}\:\mathrm{4} \\ $$$${u}={arctgx}\Rightarrow{du}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${dv}={x}^{\mathrm{2}} {dx}\Rightarrow{v}=\frac{{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${I}={uv}−\int{vdu}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {arctgx}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {arctgx}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}^{\mathrm{3}} +{x}−{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {arctgx}− \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}^{\mathrm{3}} +{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {arctgx}− \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int{xdx}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {arctvx}−\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{C} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 20/May/19
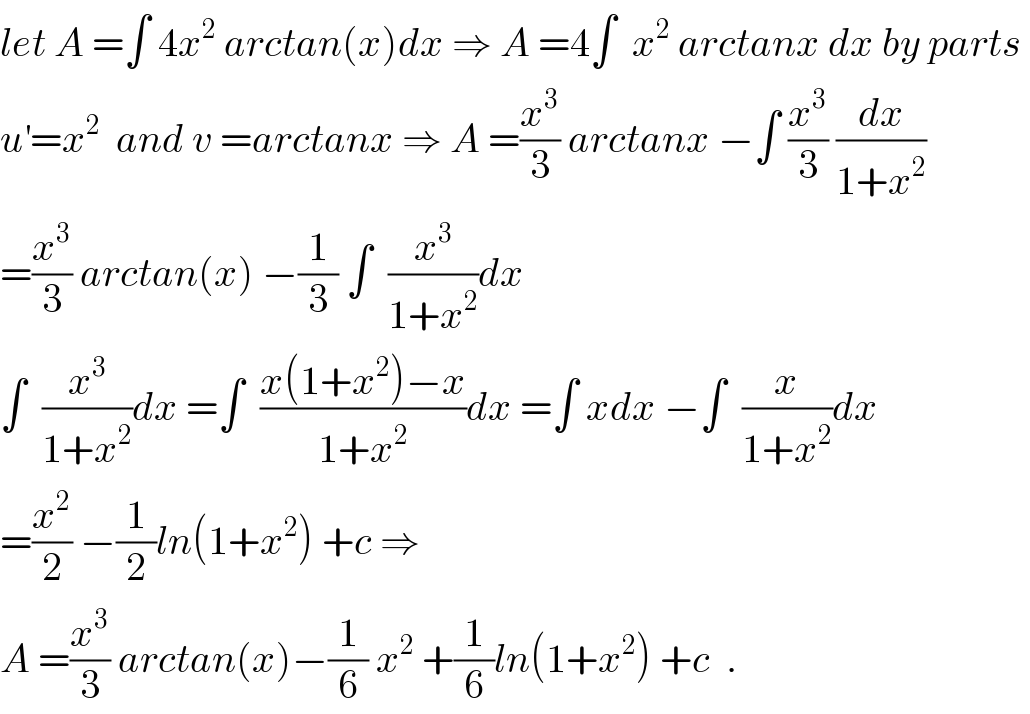
let A =∫ 4x^2 arctan(x)dx ⇒ A =4∫ x^2 arctanx dx by parts u^′ =x^2 and v =arctanx ⇒ A =(x^3 /3) arctanx −∫ (x^3 /3) (dx/(1+x^2 )) =(x^3 /3) arctan(x) −(1/3) ∫ (x^3 /(1+x^2 ))dx ∫ (x^3 /(1+x^2 ))dx =∫ ((x(1+x^2 )−x)/(1+x^2 ))dx =∫ xdx −∫ (x/(1+x^2 ))dx =(x^2 /2) −(1/2)ln(1+x^2 ) +c ⇒ A =(x^3 /3) arctan(x)−(1/6) x^2 +(1/6)ln(1+x^2 ) +c .
$${let}\:{A}\:=\int\:\mathrm{4}{x}^{\mathrm{2}} \:{arctan}\left({x}\right){dx}\:\Rightarrow\:{A}\:=\mathrm{4}\int\:\:{x}^{\mathrm{2}} \:{arctanx}\:{dx}\:{by}\:{parts}\: \\ $$$${u}^{'} ={x}^{\mathrm{2}} \:\:{and}\:{v}\:={arctanx}\:\Rightarrow\:{A}\:=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:{arctanx}\:−\int\:\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:{arctan}\left({x}\right)\:−\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int\:\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\int\:\:\frac{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\int\:{xdx}\:−\int\:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+{c}\:\Rightarrow \\ $$$${A}\:=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:{arctan}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\:{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+{c}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *