Question Number 60376 by rahul 19 last updated on 20/May/19
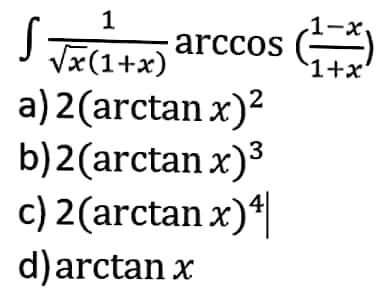
Commented by rahul 19 last updated on 20/May/19

$${dx}\:^{\ast} \\ $$
Commented by Mr X pcx last updated on 20/May/19
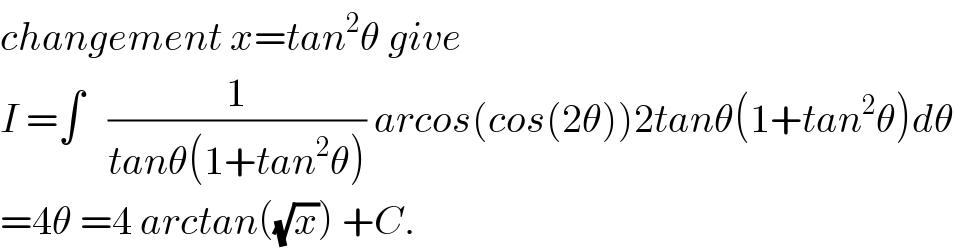
$${changement}\:{x}={tan}^{\mathrm{2}} \theta\:{give} \\ $$$${I}\:=\int\:\:\:\frac{\mathrm{1}}{{tan}\theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}\:{arcos}\left({cos}\left(\mathrm{2}\theta\right)\right)\mathrm{2}{tan}\theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\mathrm{4}\theta\:=\mathrm{4}\:{arctan}\left(\sqrt{{x}}\right)\:+{C}. \\ $$
Answered by tanmay last updated on 20/May/19
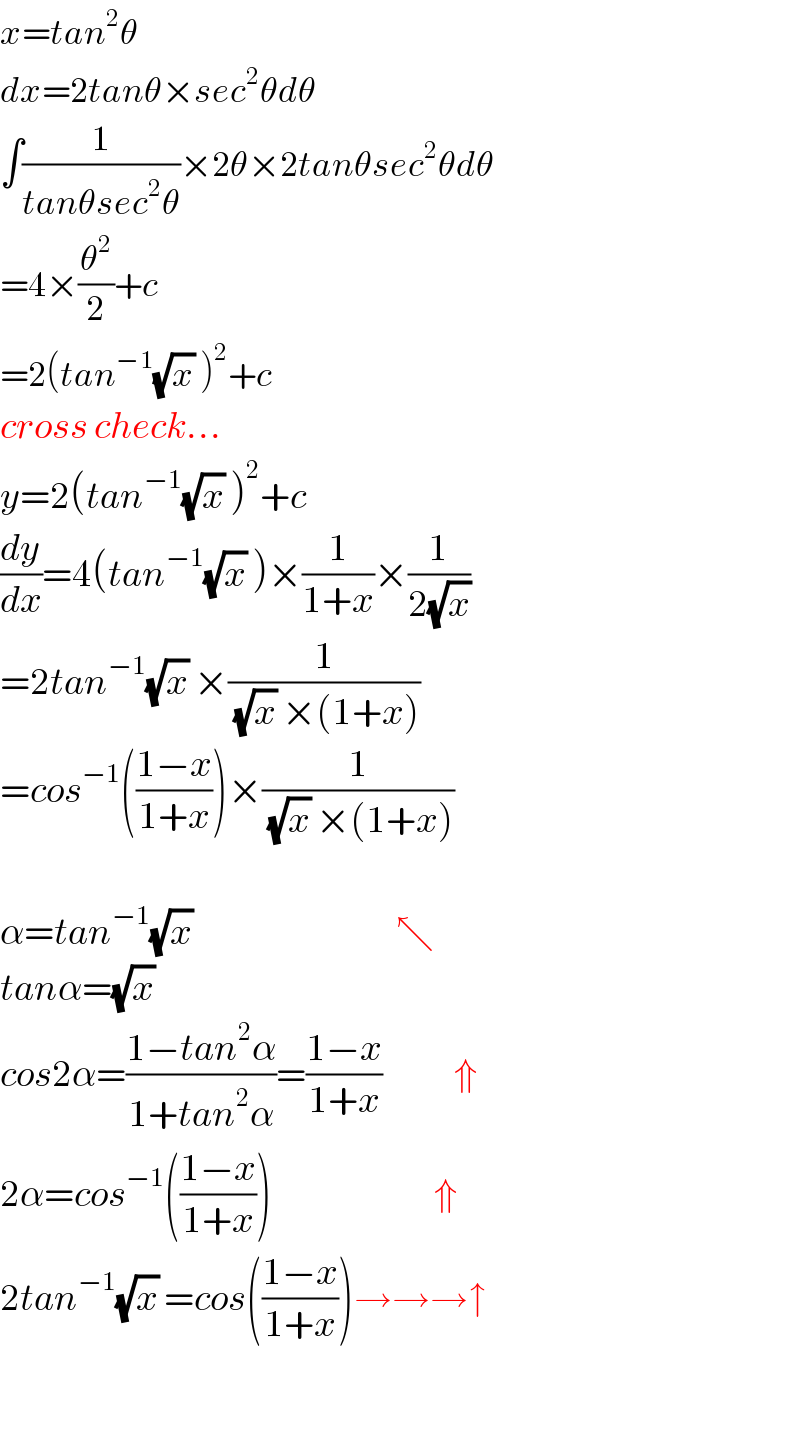
$${x}={tan}^{\mathrm{2}} \theta \\ $$$${dx}=\mathrm{2}{tan}\theta×{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\int\frac{\mathrm{1}}{{tan}\theta{sec}^{\mathrm{2}} \theta}×\mathrm{2}\theta×\mathrm{2}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\mathrm{4}×\frac{\theta^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$=\mathrm{2}\left({tan}^{−\mathrm{1}} \sqrt{{x}}\:\right)^{\mathrm{2}} +{c} \\ $$$${cross}\:{check}… \\ $$$${y}=\mathrm{2}\left({tan}^{−\mathrm{1}} \sqrt{{x}}\:\right)^{\mathrm{2}} +{c} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{4}\left({tan}^{−\mathrm{1}} \sqrt{{x}}\:\right)×\frac{\mathrm{1}}{\mathrm{1}+{x}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$$$=\mathrm{2}{tan}^{−\mathrm{1}} \sqrt{{x}}\:×\frac{\mathrm{1}}{\:\sqrt{{x}}\:×\left(\mathrm{1}+{x}\right)} \\ $$$$={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)×\frac{\mathrm{1}}{\:\sqrt{{x}}\:×\left(\mathrm{1}+{x}\right)} \\ $$$$ \\ $$$$\alpha={tan}^{−\mathrm{1}} \sqrt{{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\nwarrow \\ $$$${tan}\alpha=\sqrt{{x}}\: \\ $$$${cos}\mathrm{2}\alpha=\frac{\mathrm{1}−{tan}^{\mathrm{2}} \alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:\:\:\:\:\:\:\:\:\:\:\:\Uparrow \\ $$$$\mathrm{2}\alpha={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Uparrow \\ $$$$\mathrm{2}{tan}^{−\mathrm{1}} \sqrt{{x}}\:={cos}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\rightarrow\rightarrow\rightarrow\uparrow \\ $$$$ \\ $$
Commented by rahul 19 last updated on 20/May/19
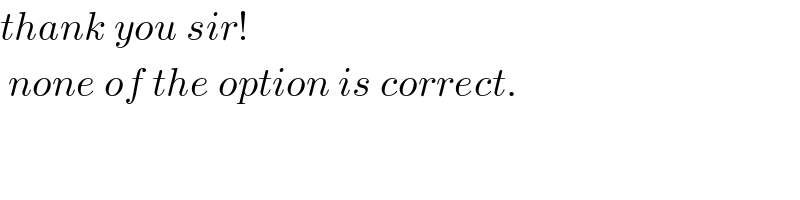
$${thank}\:{you}\:{sir}! \\ $$$$\:{none}\:{of}\:{the}\:{option}\:{is}\:{correct}. \\ $$
