Question Number 60445 by ANTARES VY last updated on 21/May/19

Commented by bhanukumarb2@gmail.com last updated on 21/May/19
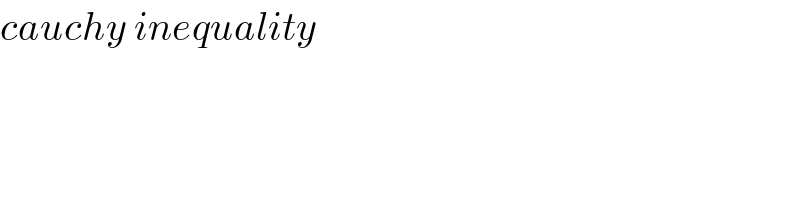
$${cauchy}\:{inequality}\: \\ $$
Answered by MJS last updated on 21/May/19
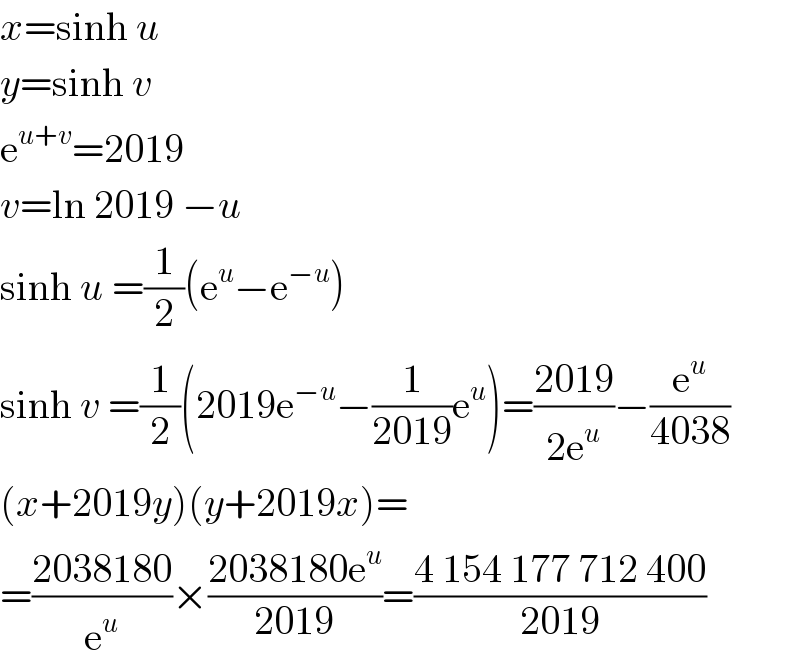
$${x}=\mathrm{sinh}\:{u} \\ $$$${y}=\mathrm{sinh}\:{v} \\ $$$$\mathrm{e}^{{u}+{v}} =\mathrm{2019} \\ $$$${v}=\mathrm{ln}\:\mathrm{2019}\:−{u} \\ $$$$\mathrm{sinh}\:{u}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{e}^{{u}} −\mathrm{e}^{−{u}} \right) \\ $$$$\mathrm{sinh}\:{v}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2019e}^{−{u}} −\frac{\mathrm{1}}{\mathrm{2019}}\mathrm{e}^{{u}} \right)=\frac{\mathrm{2019}}{\mathrm{2e}^{{u}} }−\frac{\mathrm{e}^{{u}} }{\mathrm{4038}} \\ $$$$\left({x}+\mathrm{2019}{y}\right)\left({y}+\mathrm{2019}{x}\right)= \\ $$$$=\frac{\mathrm{2038180}}{\mathrm{e}^{{u}} }×\frac{\mathrm{2038180e}^{{u}} }{\mathrm{2019}}=\frac{\mathrm{4}\:\mathrm{154}\:\mathrm{177}\:\mathrm{712}\:\mathrm{400}}{\mathrm{2019}} \\ $$
Answered by MJS last updated on 21/May/19

$${y}={x} \\ $$$$\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{2019} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{1009}}{\mathrm{2019}}\sqrt{\mathrm{2019}} \\ $$$$\left(\mathrm{2020}{x}\right)^{\mathrm{2}} =\frac{\mathrm{4}\:\mathrm{154}\:\mathrm{177}\:\mathrm{712}\:\mathrm{400}}{\mathrm{2019}} \\ $$
