Question Number 60477 by Kunal12588 last updated on 21/May/19

Answered by tanmay last updated on 21/May/19

$${v}\frac{{dv}}{{dx}}=−{k}\left({L}−{x}\right) \\ $$$${intregating} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=−{k}\left({Lx}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)+{c} \\ $$$${v}_{} ={v}_{\mathrm{0}} \:\:\:{when}\:\:{x}=\mathrm{0} \\ $$$$\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}}={c} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=−{k}\left({Lx}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{\left(\frac{{v}_{\mathrm{0}} }{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}=−{k}\left({L}×{L}−\frac{{L}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$${k}\left(\frac{{L}^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}}−\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{8}} \\ $$$${k}=\frac{\mathrm{2}}{{L}^{\mathrm{2}} }×\frac{\mathrm{3}{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{8}}=\frac{\mathrm{3}{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}{L}^{\mathrm{2}} } \\ $$$${retardation}=−{k}\left({L}−{x}\right) \\ $$$${initial}\:{retardation}=−\left(\frac{\mathrm{3}{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}{L}^{\mathrm{2}} }\right)×\left({L}−\mathrm{0}\right) \\ $$$$=\frac{−\mathrm{3}{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}{L}} \\ $$$$=\frac{−\mathrm{3}×\mathrm{25}}{\mathrm{4}×\mathrm{1}}=\frac{−\mathrm{75}}{\mathrm{4}} \\ $$$${pls}\:{check} \\ $$$$ \\ $$$$ \\ $$
Commented by Kunal12588 last updated on 21/May/19

$${Absolutely}\:{correct}\:{sir}\:{pls}\:{check}\:{my}\:{solution} \\ $$$${sir}\:{can}\:{we}\:{take}\:{x}\:{from}\:{right}\:{side}\:{i}\:{mean} \\ $$$${a}=−{kx} \\ $$
Commented by tanmay last updated on 21/May/19

$${yes}\:…. \\ $$$${complication}\:{will}\:{arise}.. \\ $$$$\left.{i}\right){time}\:{variation}\:{from}\:{left}\:{but}\:{distsnce}\:{from} \\ $$$${right}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Kunal12588 last updated on 21/May/19
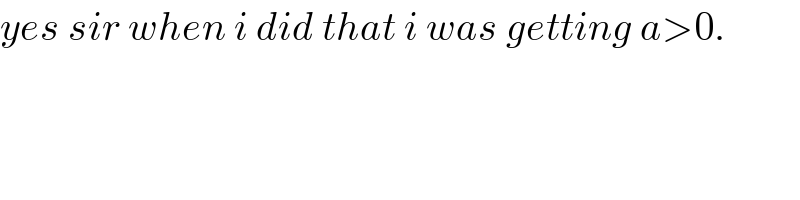
$${yes}\:{sir}\:{when}\:{i}\:{did}\:{that}\:{i}\:{was}\:{getting}\:{a}>\mathrm{0}. \\ $$
Answered by Kunal12588 last updated on 21/May/19
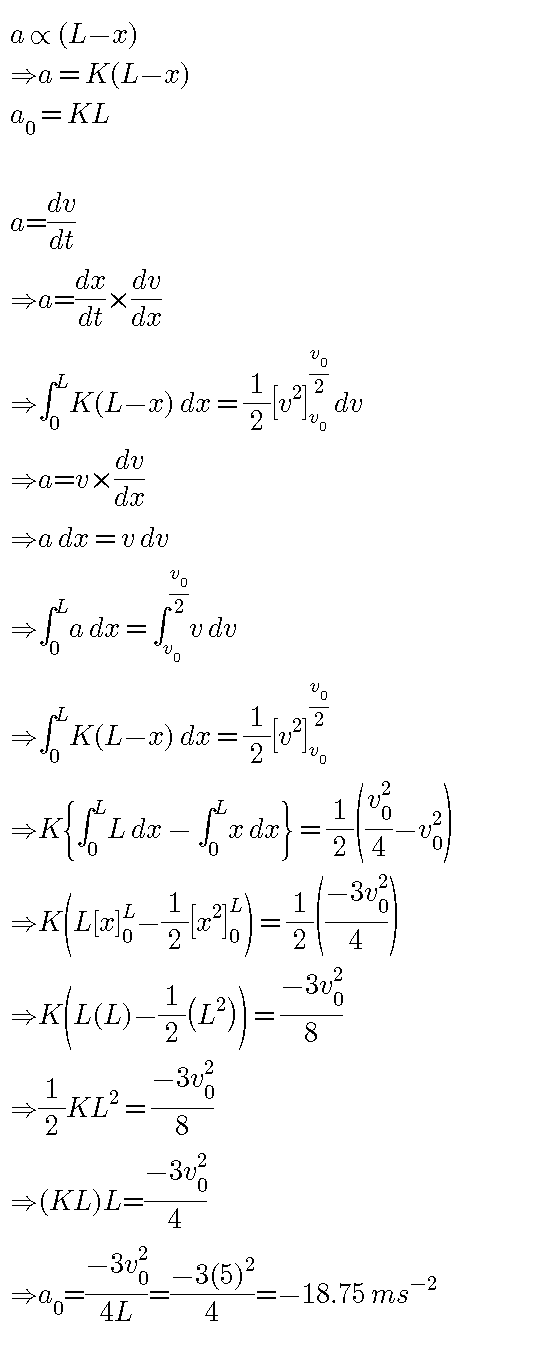
Commented by tanmay last updated on 21/May/19

$${yes}\:{correct} \\ $$
