Question Number 60510 by aliesam last updated on 21/May/19
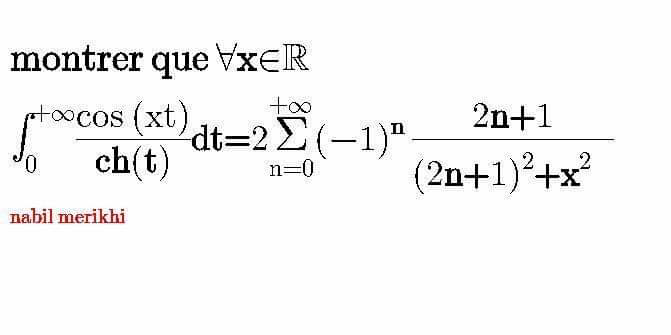
Commented by maxmathsup by imad last updated on 21/May/19
![let A =∫_0 ^∞ ((cos(xt))/(ch(t))) dt ⇒ A =∫_0 ^∞ ((cos(xt))/((e^t +e^(−t) )/2)) dt =2 ∫_0 ^∞ ((cos(xt))/(e^t +e^(−t) ))dt =2 ∫_0 ^∞ ((e^(−t) cos(xt))/(1+e^(−2t) ))dt =2 ∫_0 ^∞ e^(−t) cos(xt)(Σ_(n=0) ^∞ (−1)^n e^(−2nt) )dt =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)t) cos(xt)dt =2Σ_(n=0) ^∞ (−1)^n w_n w_n =Re ( ∫_0 ^∞ e^(−(2n+1)t) e^(ixt) dt) =Re(∫_0 ^∞ e^((ix−2n+1))t) dt) but ∫_0 ^∞ e^((ix−(2n+1))t) dt =[(1/(ix−(2n+1))) e^((ix−(2n+1))t) ]_(t=0) ^(t→+∞) =−(1/(ix−(2n+1))) =(1/((2n+1)−ix)) =((2n+1+ix)/((2n+1)^2 +x^2 )) ⇒Re(...)=((2n+1)/((2n+1)^2 +x^2 )) ⇒ A =2 Σ_(n=0) ^∞ (−1)^n ((2n+1)/((2n+1)^2 +x^2 )) .](https://www.tinkutara.com/question/Q60519.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left({xt}\right)}{{ch}\left({t}\right)}\:{dt}\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left({xt}\right)}{\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}\:{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({xt}\right)}{{e}^{{t}} \:+{e}^{−{t}} }{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−{t}} \:{cos}\left({xt}\right)}{\mathrm{1}+{e}^{−\mathrm{2}{t}} }{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−{t}} {cos}\left({xt}\right)\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{2}{nt}} \right){dt} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){t}} \:{cos}\left({xt}\right){dt}\:=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{w}_{{n}} \\ $$$${w}_{{n}} ={Re}\:\left(\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){t}} \:{e}^{{ixt}} {dt}\right)\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left.\left({ix}−\mathrm{2}{n}+\mathrm{1}\right)\right){t}} {dt}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left({ix}−\left(\mathrm{2}{n}+\mathrm{1}\right)\right){t}} {dt}\:=\left[\frac{\mathrm{1}}{{ix}−\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{e}^{\left({ix}−\left(\mathrm{2}{n}+\mathrm{1}\right)\right){t}} \right]_{{t}=\mathrm{0}} ^{{t}\rightarrow+\infty} \\ $$$$=−\frac{\mathrm{1}}{{ix}−\left(\mathrm{2}{n}+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)−{ix}}\:=\frac{\mathrm{2}{n}+\mathrm{1}+{ix}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }\:\Rightarrow{Re}\left(…\right)=\frac{\mathrm{2}{n}+\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}\:=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\frac{\mathrm{2}{n}+\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:. \\ $$
Commented by aliesam last updated on 21/May/19

$${thank}\:{you}\:{sir}\: \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 22/May/19
$${you}\:{are}\:{welcome}\:{sir} \\ $$
