Question Number 60527 by ajfour last updated on 21/May/19
Commented by ajfour last updated on 21/May/19

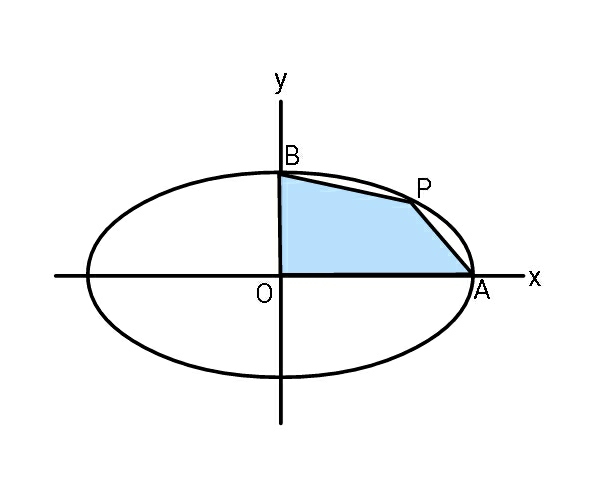
$$\mathrm{Find}\:\mathrm{maximum}\:\mathrm{area}\:\mathrm{of}\:\mathrm{quadrilateral} \\ $$$$\mathrm{OAPB}.\:\mathrm{The}\:\mathrm{ellipse}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{usual}\:\mathrm{one}. \\ $$
Answered by ajfour last updated on 22/May/19
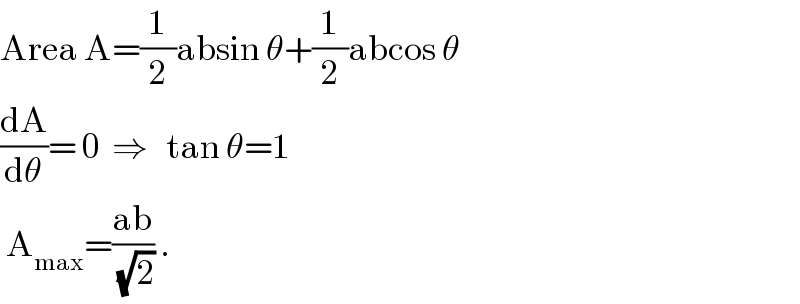
$$\mathrm{Area}\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{absin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{abcos}\:\theta \\ $$$$\frac{\mathrm{dA}}{\mathrm{d}\theta}=\:\mathrm{0}\:\:\Rightarrow\:\:\:\mathrm{tan}\:\theta=\mathrm{1} \\ $$$$\:\mathrm{A}_{\mathrm{max}} =\frac{\mathrm{ab}}{\:\sqrt{\mathrm{2}}}\:. \\ $$
Commented by mr W last updated on 22/May/19

$${thank}\:{you}\:{sir}! \\ $$
Commented by ajfour last updated on 22/May/19
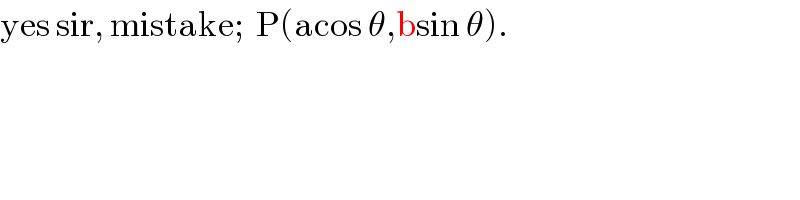
$$\mathrm{yes}\:\mathrm{sir},\:\mathrm{mistake};\:\:\mathrm{P}\left(\mathrm{acos}\:\theta,\mathrm{bsin}\:\theta\right). \\ $$
Answered by mr W last updated on 22/May/19
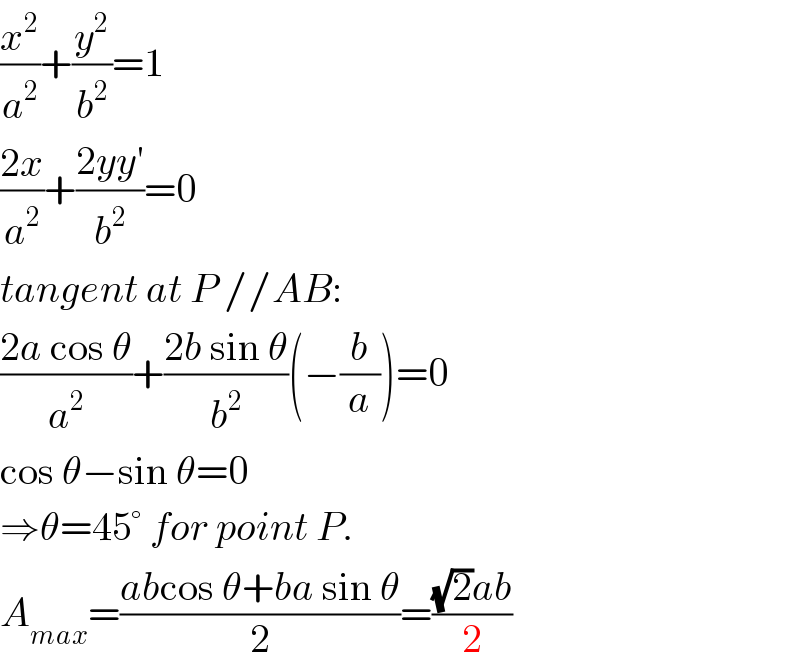
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{{a}^{\mathrm{2}} }+\frac{\mathrm{2}{yy}'}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$${tangent}\:{at}\:{P}\://{AB}: \\ $$$$\frac{\mathrm{2}{a}\:\mathrm{cos}\:\theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{2}{b}\:\mathrm{sin}\:\theta}{{b}^{\mathrm{2}} }\left(−\frac{{b}}{{a}}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\theta=\mathrm{45}°\:{for}\:{point}\:{P}. \\ $$$${A}_{{max}} =\frac{{ab}\mathrm{cos}\:\theta+{ba}\:\mathrm{sin}\:\theta}{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}{ab}}{\mathrm{2}} \\ $$
