Question-60545

Question Number 60545 by Tawa1 last updated on 21/May/19

Answered by MJS last updated on 22/May/19

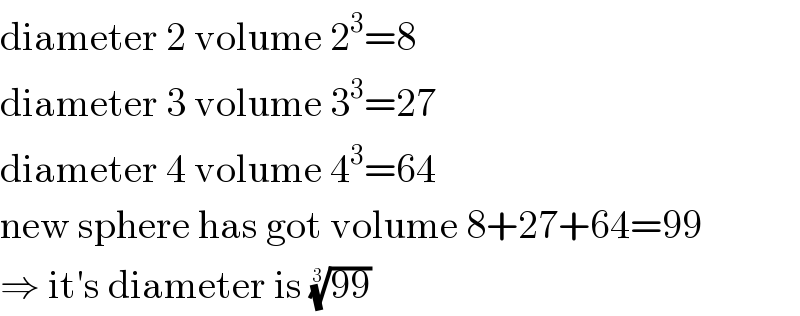
diameter 2 volume 2^3 =8 diameter 3 volume 3^3 =27 diameter 4 volume 4^3 =64 new sphere has got volume 8+27+64=99 ⇒ it′s diameter is ((99))^(1/3)

$$\mathrm{diameter}\:\mathrm{2}\:\mathrm{volume}\:\mathrm{2}^{\mathrm{3}} =\mathrm{8} \\ $$$$\mathrm{diameter}\:\mathrm{3}\:\mathrm{volume}\:\mathrm{3}^{\mathrm{3}} =\mathrm{27} \\ $$$$\mathrm{diameter}\:\mathrm{4}\:\mathrm{volume}\:\mathrm{4}^{\mathrm{3}} =\mathrm{64} \\ $$$$\mathrm{new}\:\mathrm{sphere}\:\mathrm{has}\:\mathrm{got}\:\mathrm{volume}\:\mathrm{8}+\mathrm{27}+\mathrm{64}=\mathrm{99} \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{diameter}\:\mathrm{is}\:\sqrt[{\mathrm{3}}]{\mathrm{99}} \\ $$

Commented by MJS last updated on 22/May/19

we don′t need the exact formula V=((4π)/3)r^3 =(π/6)d^3 because the factor (π/6) will be omitted at the end: (π/6)d_1 ^3 +(π/6)d_2 ^3 +(π/6)d_3 ^3 =(π/6)d_4 ^3 ⇒ d_4 =((d_1 ^3 +d_2 ^3 +d_3 ^3 ))^(1/3)

$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{formula} \\ $$$${V}=\frac{\mathrm{4}\pi}{\mathrm{3}}{r}^{\mathrm{3}} =\frac{\pi}{\mathrm{6}}{d}^{\mathrm{3}} \\ $$$$\mathrm{because}\:\mathrm{the}\:\mathrm{factor}\:\frac{\pi}{\mathrm{6}}\:\mathrm{will}\:\mathrm{be}\:\mathrm{omitted}\:\mathrm{at}\:\mathrm{the} \\ $$$$\mathrm{end}: \\ $$$$\frac{\pi}{\mathrm{6}}{d}_{\mathrm{1}} ^{\mathrm{3}} +\frac{\pi}{\mathrm{6}}{d}_{\mathrm{2}} ^{\mathrm{3}} +\frac{\pi}{\mathrm{6}}{d}_{\mathrm{3}} ^{\mathrm{3}} =\frac{\pi}{\mathrm{6}}{d}_{\mathrm{4}} ^{\mathrm{3}} \:\Rightarrow\:{d}_{\mathrm{4}} =\sqrt[{\mathrm{3}}]{{d}_{\mathrm{1}} ^{\mathrm{3}} +{d}_{\mathrm{2}} ^{\mathrm{3}} +{d}_{\mathrm{3}} ^{\mathrm{3}} } \\ $$

Commented by Tawa1 last updated on 22/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply