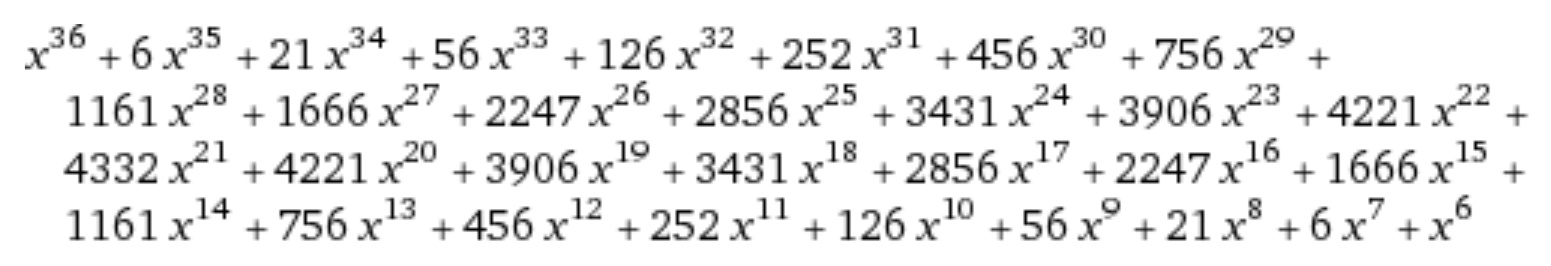Question Number 60635 by naka3546 last updated on 23/May/19
Answered by MJS last updated on 23/May/19

$$\mathrm{we}\:\mathrm{have}\:\mathrm{6}^{\mathrm{6}} =\mathrm{46656}\:\mathrm{possible}\:\mathrm{results} \\ $$$$\mathrm{33}= \\ $$$$\mathrm{666663}\:\Rightarrow\:\mathrm{6}\:\mathrm{permutations} \\ $$$$\mathrm{666654}\:\Rightarrow\:\mathrm{30}\:\mathrm{permutations} \\ $$$$\mathrm{666555}\:\Rightarrow\:\mathrm{20}\:\mathrm{permutations} \\ $$$$\Rightarrow\:\mathrm{probability}\:\mathrm{of}\:\mathrm{sum}=\mathrm{33}\:\mathrm{is}\:\frac{\mathrm{56}}{\mathrm{46656}}=\frac{\mathrm{7}}{\mathrm{5832}} \\ $$
Answered by mr W last updated on 23/May/19
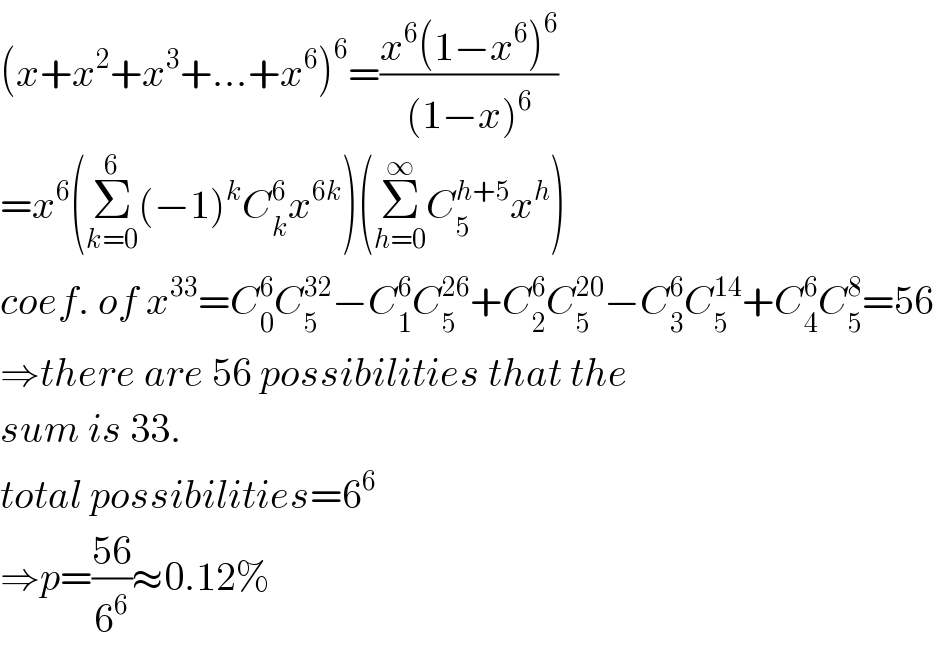
$$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{6}} \right)^{\mathrm{6}} =\frac{{x}^{\mathrm{6}} \left(\mathrm{1}−{x}^{\mathrm{6}} \right)^{\mathrm{6}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{6}} } \\ $$$$={x}^{\mathrm{6}} \left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{\mathrm{6}} {x}^{\mathrm{6}{k}} \right)\left(\underset{{h}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{5}} ^{{h}+\mathrm{5}} {x}^{{h}} \right) \\ $$$${coef}.\:{of}\:{x}^{\mathrm{33}} ={C}_{\mathrm{0}} ^{\mathrm{6}} {C}_{\mathrm{5}} ^{\mathrm{32}} −{C}_{\mathrm{1}} ^{\mathrm{6}} {C}_{\mathrm{5}} ^{\mathrm{26}} +{C}_{\mathrm{2}} ^{\mathrm{6}} {C}_{\mathrm{5}} ^{\mathrm{20}} −{C}_{\mathrm{3}} ^{\mathrm{6}} {C}_{\mathrm{5}} ^{\mathrm{14}} +{C}_{\mathrm{4}} ^{\mathrm{6}} {C}_{\mathrm{5}} ^{\mathrm{8}} =\mathrm{56} \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{56}\:{possibilities}\:{that}\:{the} \\ $$$${sum}\:{is}\:\mathrm{33}. \\ $$$${total}\:{possibilities}=\mathrm{6}^{\mathrm{6}} \\ $$$$\Rightarrow{p}=\frac{\mathrm{56}}{\mathrm{6}^{\mathrm{6}} }\approx\mathrm{0}.\mathrm{12\%} \\ $$
Commented by mr W last updated on 24/May/19