Question Number 60697 by ajfour last updated on 24/May/19
Commented by ajfour last updated on 24/May/19

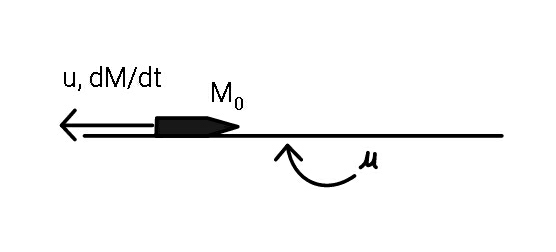
$${How}\:{far}\:{can}\:{the}\:{slider}\:{slide}\:{if}\:{it} \\ $$$${ejects}\:{mass}\:{at}\:{rate}\:\frac{{dM}}{{dt}}\:=\:{R}\:,\:{at}\:{a} \\ $$$${relative}\:{speed}\:{u}\:?\: \\ $$$$\left(\frac{{M}_{\mathrm{0}} }{\mathrm{2}}\:\:{of}\:{M}_{\mathrm{0}} \:{doesn}'{t}\:{burn}\:{and}\right. \\ $$$$\left.{assume}\:\mu\:{sufficiently}\:{less}\right) \\ $$
Answered by mr W last updated on 25/May/19
![phase 1: t=0 to t_1 , slider ejects material (dM/dt)=−R ⇒M=M_0 −Rt −μMg−u(dM/dt)=Ma −μMg+uR=Ma ⇒a=((uR)/M)−μg a=(dv/dt)=(dv/dM)×(dM/dt)=−R(dv/dM) −R(dv/dM)=((uR)/M)−μg −∫_0 ^( v) Rdv=∫_M_0 ^( M) (((uR)/M)−μg)dM −Rv=[uR ln M−μgM]_M_0 ^M ⇒v=−u ln (M/M_0 )−((μg)/R)(M_0 −M) v=(ds/dt)=(ds/dM)×(dM/dt)=−R(ds/dM) ⇒−R (ds/dM)=−u ln (M/M_0 )−((μg)/R)(M_0 −M) ⇒R∫_0 ^( s) ds=∫_M_0 ^( M) {u ln (M/M_0 )+((μg)/R)(M_0 −M)}dM ⇒Rs=uM_0 [(ln (M/M_0 )−1)(M/M_0 )]_M_0 ^M −((μg)/(2R))[(M_0 −M)^2 ]_M_0 ^M ⇒s=((uM_0 )/R) [(ln (M/M_0 )−1)(M/M_0 )+1]−((μg)/(2R^2 ))(M_0 −M)^2 at t=t_1 =(M_0 /(2R)), M=(M_0 /2): ⇒s_1 =[4(1−ln 2)uR −μgM_0 ](M_0 /(8R^2 )) ⇒v_1 =u ln 2−((μgM_0 )/(2R)) M_1 =(M_0 /2) phase 2: t=t_1 to t_2 , slider doesn′t ejects material after this point it slides s_2 till it stops, and its kinetic energy is completely lost due to friction. (1/2)M_1 v_1 ^2 =μM_1 gs_2 ⇒s_2 =(v_1 ^2 /(2μg))=(1/(2μg))(u ln 2−((μgM_0 )/(2R)))^2 total slide distance l=s_1 +s_2 ⇒l=[4(1−ln 2)uR −μgM_0 ](M_0 /(8R^2 ))+(1/(2μg))(u ln 2−((μgM_0 )/(2R)))^2 ⇒l=(((ln 2)^2 u^2 )/(2μg))−(((2ln 2−1)uM_0 )/(2R))](https://www.tinkutara.com/question/Q60709.png)
$${phase}\:\mathrm{1}:\:{t}=\mathrm{0}\:{to}\:{t}_{\mathrm{1}} ,\:{slider}\:{ejects}\:{material} \\ $$$$\frac{{dM}}{{dt}}=−{R} \\ $$$$\Rightarrow{M}={M}_{\mathrm{0}} −{Rt} \\ $$$$−\mu{Mg}−{u}\frac{{dM}}{{dt}}={Ma} \\ $$$$−\mu{Mg}+{uR}={Ma} \\ $$$$\Rightarrow{a}=\frac{{uR}}{{M}}−\mu{g} \\ $$$${a}=\frac{{dv}}{{dt}}=\frac{{dv}}{{dM}}×\frac{{dM}}{{dt}}=−{R}\frac{{dv}}{{dM}} \\ $$$$−{R}\frac{{dv}}{{dM}}=\frac{{uR}}{{M}}−\mu{g} \\ $$$$−\int_{\mathrm{0}} ^{\:{v}} {Rdv}=\int_{{M}_{\mathrm{0}} } ^{\:{M}} \left(\frac{{uR}}{{M}}−\mu{g}\right){dM} \\ $$$$−{Rv}=\left[{uR}\:\mathrm{ln}\:{M}−\mu{gM}\right]_{{M}_{\mathrm{0}} } ^{{M}} \\ $$$$\Rightarrow{v}=−{u}\:\mathrm{ln}\:\frac{{M}}{{M}_{\mathrm{0}} }−\frac{\mu{g}}{{R}}\left({M}_{\mathrm{0}} −{M}\right) \\ $$$${v}=\frac{{ds}}{{dt}}=\frac{{ds}}{{dM}}×\frac{{dM}}{{dt}}=−{R}\frac{{ds}}{{dM}} \\ $$$$\Rightarrow−{R}\:\frac{{ds}}{{dM}}=−{u}\:\mathrm{ln}\:\frac{{M}}{{M}_{\mathrm{0}} }−\frac{\mu{g}}{{R}}\left({M}_{\mathrm{0}} −{M}\right) \\ $$$$\Rightarrow{R}\int_{\mathrm{0}} ^{\:{s}} {ds}=\int_{{M}_{\mathrm{0}} } ^{\:{M}} \left\{{u}\:\mathrm{ln}\:\frac{{M}}{{M}_{\mathrm{0}} }+\frac{\mu{g}}{{R}}\left({M}_{\mathrm{0}} −{M}\right)\right\}{dM} \\ $$$$\Rightarrow{Rs}={uM}_{\mathrm{0}} \:\left[\left(\mathrm{ln}\:\frac{{M}}{{M}_{\mathrm{0}} }−\mathrm{1}\right)\frac{{M}}{{M}_{\mathrm{0}} }\right]_{{M}_{\mathrm{0}} } ^{{M}} −\frac{\mu{g}}{\mathrm{2}{R}}\left[\left({M}_{\mathrm{0}} −{M}\right)^{\mathrm{2}} \right]_{{M}_{\mathrm{0}} } ^{{M}} \\ $$$$\Rightarrow{s}=\frac{{uM}_{\mathrm{0}} }{{R}}\:\left[\left(\mathrm{ln}\:\frac{{M}}{{M}_{\mathrm{0}} }−\mathrm{1}\right)\frac{{M}}{{M}_{\mathrm{0}} }+\mathrm{1}\right]−\frac{\mu{g}}{\mathrm{2}{R}^{\mathrm{2}} }\left({M}_{\mathrm{0}} −{M}\right)^{\mathrm{2}} \\ $$$${at}\:{t}={t}_{\mathrm{1}} =\frac{{M}_{\mathrm{0}} }{\mathrm{2}{R}},\:{M}=\frac{{M}_{\mathrm{0}} }{\mathrm{2}}: \\ $$$$\Rightarrow{s}_{\mathrm{1}} =\left[\mathrm{4}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right){uR}\:−\mu{gM}_{\mathrm{0}} \right]\frac{{M}_{\mathrm{0}} }{\mathrm{8}{R}^{\mathrm{2}} } \\ $$$$\Rightarrow{v}_{\mathrm{1}} ={u}\:\mathrm{ln}\:\mathrm{2}−\frac{\mu{gM}_{\mathrm{0}} }{\mathrm{2}{R}} \\ $$$${M}_{\mathrm{1}} =\frac{{M}_{\mathrm{0}} }{\mathrm{2}} \\ $$$${phase}\:\mathrm{2}:\:{t}={t}_{\mathrm{1}} \:{to}\:{t}_{\mathrm{2}} ,\:{slider}\:{doesn}'{t}\:{ejects}\:{material} \\ $$$${after}\:{this}\:{point}\:{it}\:{slides}\:{s}_{\mathrm{2}} \:{till}\:{it}\:{stops}, \\ $$$${and}\:{its}\:{kinetic}\:{energy}\:{is}\:{completely} \\ $$$${lost}\:{due}\:{to}\:{friction}. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{M}_{\mathrm{1}} {v}_{\mathrm{1}} ^{\mathrm{2}} =\mu{M}_{\mathrm{1}} {gs}_{\mathrm{2}} \\ $$$$\Rightarrow{s}_{\mathrm{2}} =\frac{{v}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\mu{g}}=\frac{\mathrm{1}}{\mathrm{2}\mu{g}}\left({u}\:\mathrm{ln}\:\mathrm{2}−\frac{\mu{gM}_{\mathrm{0}} }{\mathrm{2}{R}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${total}\:{slide}\:{distance} \\ $$$${l}={s}_{\mathrm{1}} +{s}_{\mathrm{2}} \\ $$$$\Rightarrow{l}=\left[\mathrm{4}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right){uR}\:−\mu{gM}_{\mathrm{0}} \right]\frac{{M}_{\mathrm{0}} }{\mathrm{8}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\mu{g}}\left({u}\:\mathrm{ln}\:\mathrm{2}−\frac{\mu{gM}_{\mathrm{0}} }{\mathrm{2}{R}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{l}=\frac{\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} {u}^{\mathrm{2}} }{\mathrm{2}\mu{g}}−\frac{\left(\mathrm{2ln}\:\mathrm{2}−\mathrm{1}\right){uM}_{\mathrm{0}} }{\mathrm{2}{R}} \\ $$
Commented by ajfour last updated on 25/May/19

$${Very}\:\mathcal{G}{ood}\:{Sir},\:{elaborate}\:{and}\:{wise}! \\ $$
