Question Number 60716 by peter frank last updated on 24/May/19

Commented by maxmathsup by imad last updated on 25/May/19
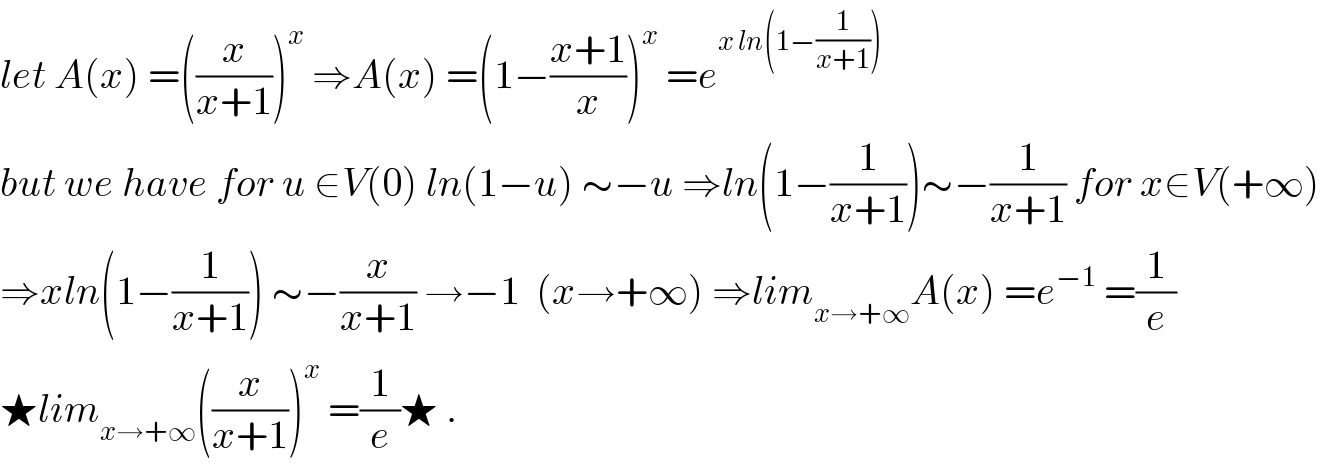
$${let}\:{A}\left({x}\right)\:=\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{{x}} \:\Rightarrow{A}\left({x}\right)\:=\left(\mathrm{1}−\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}} \:={e}^{{x}\:{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)} \\ $$$${but}\:{we}\:{have}\:{for}\:{u}\:\in{V}\left(\mathrm{0}\right)\:{ln}\left(\mathrm{1}−{u}\right)\:\sim−{u}\:\Rightarrow{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\sim−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:{for}\:{x}\in{V}\left(+\infty\right) \\ $$$$\Rightarrow{xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\:\sim−\frac{{x}}{{x}+\mathrm{1}}\:\rightarrow−\mathrm{1}\:\:\left({x}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {A}\left({x}\right)\:={e}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{{e}} \\ $$$$\bigstar{lim}_{{x}\rightarrow+\infty} \left(\frac{{x}}{{x}+\mathrm{1}}\right)^{{x}} \:=\frac{\mathrm{1}}{{e}}\bigstar\:. \\ $$
Answered by Smail last updated on 24/May/19
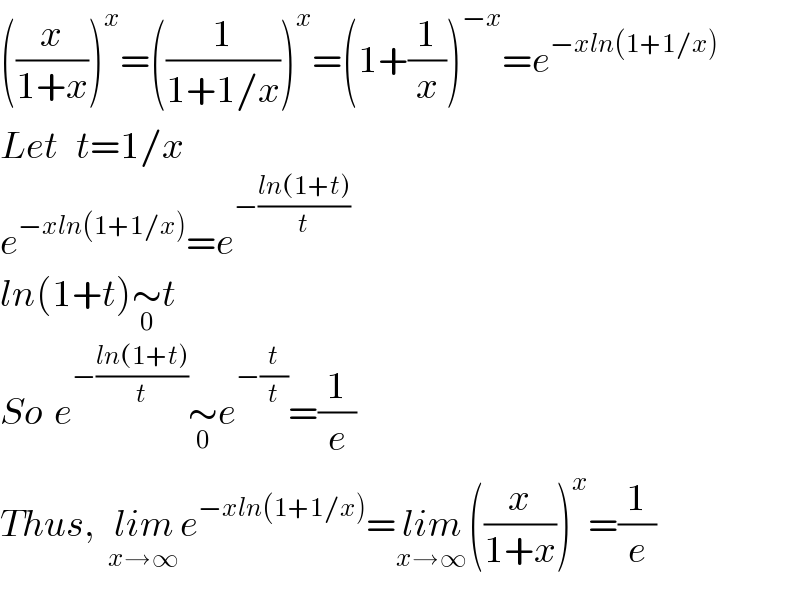
$$\left(\frac{{x}}{\mathrm{1}+{x}}\right)^{{x}} =\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}/{x}}\right)^{{x}} =\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{−{x}} ={e}^{−{xln}\left(\mathrm{1}+\mathrm{1}/{x}\right)} \\ $$$${Let}\:\:\:{t}=\mathrm{1}/{x} \\ $$$${e}^{−{xln}\left(\mathrm{1}+\mathrm{1}/{x}\right)} ={e}^{−\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}} \\ $$$${ln}\left(\mathrm{1}+{t}\right)\underset{\mathrm{0}} {\sim}{t} \\ $$$${So}\:\:{e}^{−\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}} \underset{\mathrm{0}} {\sim}{e}^{−\frac{{t}}{{t}}} =\frac{\mathrm{1}}{{e}} \\ $$$${Thus},\:\:\underset{{x}\rightarrow\infty} {{lim}e}^{−{xln}\left(\mathrm{1}+\mathrm{1}/{x}\right)} =\underset{{x}\rightarrow\infty} {{lim}}\left(\frac{{x}}{\mathrm{1}+{x}}\right)^{{x}} =\frac{\mathrm{1}}{{e}} \\ $$
Commented by peter frank last updated on 24/May/19

$${thank}\:{you} \\ $$
